2025年期中期末名校名区真题精编高一数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年期中期末名校名区真题精编高一数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
16. (15分)某地为了帮扶中小微企业纾困解难,给予企业一定的专项贷款资金支持.如图是该地120家中小微企业的专项贷款金额(万元)的频率分布直方图:
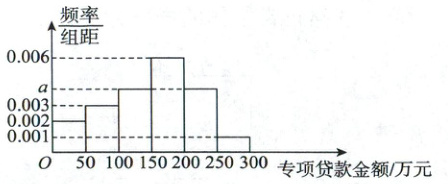
(1)确定$a$的值,并估计这120家中小微企业的专项贷款金额的中位数(结果保留整数).
(2)按专项贷款金额进行分层抽样,从这120家中小微企业中随机抽取20家,记专项贷款金额在$[200,300]$内应抽取的中小微企业数为$m$.
①求$m$的值;
②从这$m$家中小微企业中随机抽取3家,求这3家中小微企业的专项贷款金额都在$[200,250)$内的概率.

(1)确定$a$的值,并估计这120家中小微企业的专项贷款金额的中位数(结果保留整数).
(2)按专项贷款金额进行分层抽样,从这120家中小微企业中随机抽取20家,记专项贷款金额在$[200,300]$内应抽取的中小微企业数为$m$.
①求$m$的值;
②从这$m$家中小微企业中随机抽取3家,求这3家中小微企业的专项贷款金额都在$[200,250)$内的概率.
答案:
16.[解析] 本题考查频率分布直方图、分层抽样、概率
(1)根据频率分布直方图所有小矩形面积之和为1得(0.002 + 0.003 + a + 0.006 + a + 0.001)×50 = 1,解得a = 0.004.设中位数为t,易知专项贷款金额在[0,150)内的频率为0.45,在[0,200)内的频率为0.75,所以t在[150,200)内,则(t - 150)×0.006 = 0.5 - 0.45,解得t≈158,所以a的值为0.004,估计这120家中小微企业的专项贷款金额的中位数为158万元.
(2)①由题意,得抽样比为$\frac{20}{120}$ = $\frac{1}{6}$,专项贷款金额在[200,300]内的中小微企业共有120×50×(0.004 + 0.001) = 30(家),所以应该抽取30×$\frac{1}{6}$ = 5(家),即m = 5,故m的值为5.
②易知专项贷款金额在[200,250)内和在[250,300]内的频率之比为4:1,故在抽取的5家中小微企业中,专项贷款金额在[200,250)内的有5×$\frac{4}{5}$ = 4(家),分别记为A,B,C,D,专项贷款金额在[250,300]内的有5×$\frac{1}{5}$ = 1(家),记为E,从这5家中小微企业中随机抽取3家的可能情况有ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE,共10种,其中这3家中小微企业的专项贷款金额都在[200,250)内的情况有ABC,ABD,ACD,BCD,共4种,所以所求概率P = $\frac{4}{10}$ = $\frac{2}{5}$,故从这5家中小微企业中随机抽取3家,这3家中小微企业的专项贷款金额都在[200,250)内的概率为$\frac{2}{5}$.
(1)根据频率分布直方图所有小矩形面积之和为1得(0.002 + 0.003 + a + 0.006 + a + 0.001)×50 = 1,解得a = 0.004.设中位数为t,易知专项贷款金额在[0,150)内的频率为0.45,在[0,200)内的频率为0.75,所以t在[150,200)内,则(t - 150)×0.006 = 0.5 - 0.45,解得t≈158,所以a的值为0.004,估计这120家中小微企业的专项贷款金额的中位数为158万元.
(2)①由题意,得抽样比为$\frac{20}{120}$ = $\frac{1}{6}$,专项贷款金额在[200,300]内的中小微企业共有120×50×(0.004 + 0.001) = 30(家),所以应该抽取30×$\frac{1}{6}$ = 5(家),即m = 5,故m的值为5.
②易知专项贷款金额在[200,250)内和在[250,300]内的频率之比为4:1,故在抽取的5家中小微企业中,专项贷款金额在[200,250)内的有5×$\frac{4}{5}$ = 4(家),分别记为A,B,C,D,专项贷款金额在[250,300]内的有5×$\frac{1}{5}$ = 1(家),记为E,从这5家中小微企业中随机抽取3家的可能情况有ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE,共10种,其中这3家中小微企业的专项贷款金额都在[200,250)内的情况有ABC,ABD,ACD,BCD,共4种,所以所求概率P = $\frac{4}{10}$ = $\frac{2}{5}$,故从这5家中小微企业中随机抽取3家,这3家中小微企业的专项贷款金额都在[200,250)内的概率为$\frac{2}{5}$.
17. (15分)已知函数$f(x)=\log_ax(a>0$,且$a\neq1)$,若函数$f(x)$在区间$[1,4]$上的最大值与最小值之和为2.
(1)求函数$f(x)$的解析式,并求出关于$x$的不等式$f(\frac{x - 1}{x + 1})<1$的解集;
(2)求函数$g(x)=f(\frac{x}{4})· f(2x)$,$x\in[1,4]$的值域,并求出取得最值时对应的$x$的值.
(1)求函数$f(x)$的解析式,并求出关于$x$的不等式$f(\frac{x - 1}{x + 1})<1$的解集;
(2)求函数$g(x)=f(\frac{x}{4})· f(2x)$,$x\in[1,4]$的值域,并求出取得最值时对应的$x$的值.
答案:
17.[解析] 本题考查对数函数的性质及应用
(1)函数f(x) = logₐx的定义域为(0,+∞),且f(x)在(0,+∞)上单调,由函数f(x)在区间[1,4]上的最大值与最小值之和为2,得logₐ1 + logₐ4 = 2,即2logₐ2 = 2logₐa,解得a = 2,所以函数f(x)的解析式为f(x) = log₂x.f($\frac{x - 1}{x + 1}$)<1⇔log₂$\frac{x - 1}{x + 1}$<log₂2⇔0<$\frac{x - 1}{x + 1}$<2,解不等式$\frac{x - 1}{x + 1}$>0,得x< - 1或x>1,解不等式$\frac{x - 1}{x + 1}$<2,即$\frac{x + 3}{x + 1}$>0,得x< - 3或x> - 1,因此x< - 3或x>1,所以不等式f($\frac{x - 1}{x + 1}$)<1的解集为{x|x< - 3或x>1}.
(2)由
(1)知,f(x) = log₂x,则g(x) = f($\frac{x}{4}$)·f(2x) = log₂$\frac{x}{4}$·log₂2x = (log₂x - 2)·(log₂x + 1) = (log₂x)² - log₂x - 2.令log₂x = t,由x∈[1,4],得t∈[0,2],令h(t) = t² - t - 2 = (t - $\frac{1}{2}$)² - $\frac{9}{4}$,t∈[0,2],当t = $\frac{1}{2}$时,h(t)ₘᵢₙ = -$\frac{9}{4}$,此时x = $\sqrt{2}$,当t = 2时,h(t)ₘₐₓ = 0,此时x = 4,所以函数g(x)的值域为[-$\frac{9}{4}$,0],取最小值时x = $\sqrt{2}$,取最大值时x = 4.
(1)函数f(x) = logₐx的定义域为(0,+∞),且f(x)在(0,+∞)上单调,由函数f(x)在区间[1,4]上的最大值与最小值之和为2,得logₐ1 + logₐ4 = 2,即2logₐ2 = 2logₐa,解得a = 2,所以函数f(x)的解析式为f(x) = log₂x.f($\frac{x - 1}{x + 1}$)<1⇔log₂$\frac{x - 1}{x + 1}$<log₂2⇔0<$\frac{x - 1}{x + 1}$<2,解不等式$\frac{x - 1}{x + 1}$>0,得x< - 1或x>1,解不等式$\frac{x - 1}{x + 1}$<2,即$\frac{x + 3}{x + 1}$>0,得x< - 3或x> - 1,因此x< - 3或x>1,所以不等式f($\frac{x - 1}{x + 1}$)<1的解集为{x|x< - 3或x>1}.
(2)由
(1)知,f(x) = log₂x,则g(x) = f($\frac{x}{4}$)·f(2x) = log₂$\frac{x}{4}$·log₂2x = (log₂x - 2)·(log₂x + 1) = (log₂x)² - log₂x - 2.令log₂x = t,由x∈[1,4],得t∈[0,2],令h(t) = t² - t - 2 = (t - $\frac{1}{2}$)² - $\frac{9}{4}$,t∈[0,2],当t = $\frac{1}{2}$时,h(t)ₘᵢₙ = -$\frac{9}{4}$,此时x = $\sqrt{2}$,当t = 2时,h(t)ₘₐₓ = 0,此时x = 4,所以函数g(x)的值域为[-$\frac{9}{4}$,0],取最小值时x = $\sqrt{2}$,取最大值时x = 4.
查看更多完整答案,请扫码查看


