《2025年期中期末名校名区真题精编高一数学上册人教版》

10. 给出下列结论，其中正确的结论是（CD）
A.函数 $y = \left(\frac{1}{2}\right)^{-x^{2}+1}$ 的最大值为 $\frac{1}{2}$
B.已知函数 $y = \log_{a}(2 - ax)$（$a\gt0$ 且 $a\neq1$）在 $(0,1)$ 上是减函数，则实数 $a$ 的取值范围是 $(1,2)$
C.函数 $f(x)$ 满足 $f(x)-2f(-x)=2x - 1$，则 $f(3)=3$
D.已知定义在 $\mathbf{R}$ 上的奇函数 $f(x)$ 在 $(-\infty,0)$ 内有 1010 个零点，则函数 $f(x)$ 的零点个数为 2021

答案： 10.CD 本题考查复合函数和抽象函数的性质 对于A，因为-x²+1≤1，所以($\frac{1}{2}$)⁻ˣ²⁺¹≥$\frac{1}{2}$，因此y = ($\frac{1}{2}$)⁻ˣ²⁺¹有最小值$\frac{1}{2}$，无最大值，所以A不正确；对于B，因为函数y=logₐ(2 - ax)(a＞0且a≠1)在(0,1)上是减函数，所以$\begin{cases}a＞1\\2 - a\geqslant0\end{cases}$，解得1＜a≤2，所以实数a的取值范围是(1,2]，所以B不正确；对于C，由$\begin{cases}f(x)-2f(-x)=2x - 1\\f(-x)-2f(x)=-2x - 1\end{cases}$，得f(x)=$\frac{2}{3}$x + 1，所以f
(3)=3，所以C正确；对于D，因为定义在R上的奇函数f(x)在(-∞,0)内有1010个零点，所以函数f(x)在(0,+∞)内也有1010个零点，而f
(0)=0，因此函数f(x)的零点个数为2×1010 + 1 = 2021，所以D正确。故选CD。

11. 已知 $f(x)$ 为 $\mathbf{R}$ 上的奇函数，且当 $x\gt0$ 时，$f(x)=\lg x$，记 $g(x)=\sin x + f(x)·\cos x$，下列结论正确的是（ ）

A.$g(x)$ 为奇函数
B.若 $g(x)$ 的一个零点为 $x_{0}$，且 $x_{0}\lt0$，则 $\lg(-x_{0})-\tan x_{0}=0$
C.$g(x)$ 在区间 $\left(-\frac{\pi}{2},\pi\right)$ 上的零点个数为 3
D.若 $g(x)$ 大于 1 的零点从小到大依次为 $x_{1}$，$x_{2}$，$·s$，则 $7\lt x_{1}+x_{2}\lt3\pi$

答案：
11.ABD 本题考查函数的奇偶性、函数零点的判断 因为g(-x)=sin(-x)+f(-x)·cos(-x) = -sin x - f(x)·cos x=-g(x)，x∈R，关于原点对称，所以函数g(x)为奇函数，故A正确；当cos x = 0，即x=$\frac{\pi}{2}$+kπ，k∈Z时，sin x + f(x)·cos x = sin($\frac{\pi}{2}$+kπ)=cos kπ≠0，所以当x=$\frac{\pi}{2}$+kπ，k∈Z时，g(x)≠0，当x≠$\frac{\pi}{2}$+kπ，k∈Z时，sin x + f(x)·cos x=0⇔tan x=-f(x)，当x₀＜0时，-x₀＞0，则f(x₀)=-f(-x₀)=-lg(-x₀)，由于g(x)的一个零点为x₀，则tan x₀=-f(x₀)=lg(-x₀)，即lg(-x₀)-tan x₀=0，故B正确；
当x＞0时，令y₁=tan x，y₂=-lg x，则此时g(x)的零点个数为y₁=tan x与y₂=-lg x的图象的交点个数，如图，

由图可知，函数g(x)在区间(0,π)上的零点有2个，因为函数g(x)为奇函数，所以函数g(x)在区间(-$\frac{\pi}{2}$,0)上的零点有1个，并且g
(0)=sin0 + f
(0)·cos0 = 0，所以函数g(x)在区间(-$\frac{\pi}{2},\pi$)上的零点个数为4，故C不正确；由图可知，$\frac{3\pi}{4}$＜x₁＜π，$\frac{3\pi}{4}$＜x₂＜2π，所以$\frac{9\pi}{4}$＜x₁ + x₂＜3π，而$\frac{9\pi}{4}$＞7，故可得7＜x₁ + x₂＜3π，故D正确。故选ABD。

12. 衣柜里的樟脑丸，随着时间会挥发而体积缩小，刚放进的新丸体积为 $a$，经过 $t$ 天后体积 $V$ 与天数 $t$ 的关系式为 $V = a·\mathrm{e}^{-kt}$. 已知新丸经过 50 天后，体积变为 $\frac{4}{9}a$. 若一个新丸体积变为 $\frac{8}{27}a$，则需经过的天数为75.

答案： 12.75 [解析] 本题考查指数函数的应用 由已知得$\frac{4}{9}$a=a·e⁻⁵⁰ᵏ，所以e⁻ᵏ=($\frac{4}{9}$)${}^{\frac{1}{50}}$。设经过t₁天后，一个新丸体积变为$\frac{8}{27}$a，则$\frac{8}{27}$a=a·e⁻ᵏᵗ₁，所以$\frac{8}{27}$=(e⁻ᵏ)ᵗ₁=($\frac{4}{9}$)${}^{\frac{t₁}{50}}$，所以$\frac{t₁}{50}$=$\frac{3}{2}$，解得t₁=75。

13. 已知函数 $f(x)$ 的定义域为 $D$，若满足：①$f(x)$ 在 $D$ 内是单调函数；②存在 $[a,b]\subseteq D$，使 $f(x)$ 在 $[a,b]$ 上的值域为 $\left[\frac{a}{2},\frac{b}{2}\right]$，那么就称 $y = f(x)$ 为“半保值函数”. 若函数 $f(x)=\log_{a}(a^{x}+t^{2})$（$a\gt0$ 且 $a\neq1$）是“半保值函数”，则 $t$ 的取值范围为$(-\frac{1}{2},0)\cup(0,\frac{1}{2})$.

答案： 13.(-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) [解析] 本题考查函数的新定义 函数f(x)=logₐ(aˣ+t²)(a＞0且a≠1)是“半保值函数”，且定义域为R，当a＞1时，z = aˣ+t²在R上单调递增，y=logₐz在(0,+∞)上单调递增，可得f(x)为R上的增函数。当0＜a＜1时，f(x)仍为R上的增函数，所以f(x)在其定义域R内为增函数。因为函数f(x)=logₐ(aˣ+t²)与y=$\frac{1}{2}$x的图象有两个不同的交点，所以logₐ(aˣ+t²)=$\frac{1}{2}$x有两个不同的根，即aˣ+t²=a${}^{\frac{x}{2}}$有两个不同的根，即aˣ-a${}^{\frac{x}{2}}$+t²=0有两个不同的正数根，可得1 - 4t²＞0，且t²＞0，解得-$\frac{1}{2}$＜t＜0或0＜t＜$\frac{1}{2}$，所以t的取值范围为(-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$)。

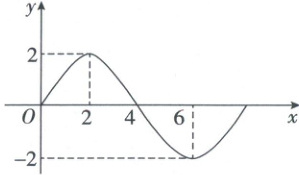
14. 函数 $f(x)=A\cos(\omega x+\varphi)$（$A\gt0$，$\omega\gt0$）的部分图象如图所示，则 $f(1)+f(2)+f(3)+·s + f(2020)+f(2021)=$2+$\sqrt{2}$.

答案： 14.2+$\sqrt{2}$ 

15. （13 分）已知函数 $f(x)=b· a^{x}$（$a$，$b$ 为常数且 $a\gt0$，$a\neq1$）的图象经过点 $A(1,8)$，$B(3,32)$.
（1）求 $a$，$b$ 的值；
（2）若不等式 $\left(\frac{1}{a}\right)^{x}+\left(\frac{1}{b}\right)^{x}-m\geq0$ 在 $x\in(-\infty,1]$ 时恒成立，求实数 $m$ 的取值范围.

答案： 15.[解析] 本题考查指数函数的性质、由不等式恒成立求参数
(1)因为函数f(x)=b·aˣ的图象经过点A(1,8)，B(3,32)，所以$\begin{cases}a· b=8\\a^{3}· b=32\end{cases}$，因为a＞0，所以a = 2，b = 4，所以f(x)=4·2ˣ=2ˣ⁺²。
(2)原不等式($\frac{1}{2}$)ˣ+($\frac{1}{4}$)ˣ-m≥0为($\frac{1}{2}$)ˣ+($\frac{1}{4}$)ˣ-m≥0，即m≤($\frac{1}{2}$)ˣ+($\frac{1}{4}$)ˣ在x∈(-∞,1]时恒成立，而y=($\frac{1}{2}$)ˣ+($\frac{1}{4}$)ˣ在x∈(-∞,1]时单调递减，故当x = 1时，y=($\frac{1}{2}$)ˣ+($\frac{1}{4}$)ˣ有最小值，为($\frac{1}{2}$)¹+($\frac{1}{4}$)¹=$\frac{3}{4}$，故m≤$\frac{3}{4}$。所以实数m的取值范围是(-∞,$\frac{3}{4}$]。