《2025年期中期末名校名区真题精编高一数学上册人教版》

16. (15 分) 若正数 $ a $，$ b $ 满足 $ a b = 4 a + b + t $，$ t \in \mathbf { R } $.
（1）当 $ t = 0 $ 时，求 $ a + 4 b $ 的最小值；
（2）当 $ t = 5 $ 时，求 $ a b $ 的取值范围.

答案： 16.[解析] 本题考查基本不等式及其应用。
(1)当t = 0时，ab = 4a + b，即$\frac{1}{a}$ + $\frac{4}{b}$ = 1，所以a + 4b=(a + 4b)($\frac{1}{a}$ + $\frac{4}{b}$)=17 + $\frac{4b}{a}$ + $\frac{4a}{b}$ ≥ 17 + 2$\sqrt{\frac{4b}{a}·\frac{4a}{b}}$ = 17 + 2×4 = 25，当且仅当$\frac{4b}{a}$ = $\frac{4a}{b}$且$\frac{1}{a}$ + $\frac{4}{b}$ = 1，即a = b = 5时取等号。故a + 4b的最小值为25。
(2)当t = 5时，ab = 4a + b + 5，即4a + b = ab - 5。因为4a + b≥2$\sqrt{4ab}$ = 4$\sqrt{ab}$，当且仅当4a = b且4a + b = ab - 5，即a = $\frac{5}{2}$，b = 10时，等号成立，所以ab - 5≥4$\sqrt{ab}$，即($\sqrt{ab}$)² - 4$\sqrt{ab}$ - 5≥0，解得$\sqrt{ab}$≥5($\sqrt{ab}$≤ -1舍去)，所以ab≥25，故ab的取值范围为[25,+∞)。

17. (15 分) 某中学学生在社会实践活动中，通过对某商店一种换季商品销售情况的调查发现：该商品在过去的两个月内（以 60 天计）的日销售价格 $ P ( x ) $（元）与时间 $ x $（天）的函数关系近似满足 $ P ( x ) = 1 + \frac { 2 } { x } $. 该商品的日销售量 $ Q ( x ) $（个）与时间 $ x $（天）的部分数据如下表所示：

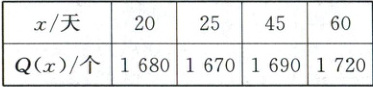
（1）请你根据上表中的数据，从中选择你认为最合适的一种函数模型来描述该商品的日销售量 $ Q ( x ) $ 与时间 $ x $ 的关系，并求出该函数的解析式；
（2）求该商品的日销售收入 $ f ( x ) $（$ 1 \leq x \leq 60 $，$ x \in \mathbf { N } ^ { * } $）的最小值.

答案： 17.[解析] 本题考查根据实际问题选择函数模型、函数的最值。
(1)选择模型②（绝对值函数模型）。设Q(x)=a|x - 30| + b，将(20,1680)，(25,1670)代入得：$\begin{cases}10a + b = 1680\\5a + b = 1670\end{cases}$，解得$\begin{cases}a = 2\\b = 1660\end{cases}$，所以Q(x)=2|x - 30| + 1660。验证x=45时，Q
(45)=2×15 + 1660=1690；x=60时，Q
(60)=2×30 + 1660=1720，均符合表中数据，故Q(x)=2|x - 30| + 1660（1≤x≤60，x∈N*）。
(2)当1≤x≤30时，Q(x)=1720 - 2x，f(x)=P(x)Q(x)=(1 + $\frac{2}{x}$)(1720 - 2x)=1720 - 2x + $\frac{3440}{x}$ - 4=1716 - 2x + $\frac{3440}{x}$，在[1,30]上单调递减，最小值为f
(30)=1716 - 60 + $\frac{3440}{30}$≈1771；当30＜x≤6０时，Q(x)=2x + 1600，f(x)=(1 + $\frac{2}{x}$)(2x + 1600)=2x + 1600 + 4 + $\frac{3200}{x}$=2x + $\frac{3200}{x}$ + 1604，在(30,40]递减，[40,60]递增，最小值为f
(40)=80 + 80 + 1604=1764。比较得日销售收入最小值为1764元。