《2025年期中期末名校名区真题精编高一数学上册人教版》

1. 已知集合 $ A = \{ 1,2,3 \} $，那么 $ A $ 的子集的个数是（8）
A.8
B.7
C.4
D.3

答案： 1. A 本题考查元素个数与子集个数的关系 集合 $\text { A } =$$\langle 1 , 2 , 3 \rangle$,则集合 A 的子集共有 $2 ^ { 3 } = 8 ( \uparrow )$. 故选 A.

2. 命题：“$ \exists x \in \mathbf{R},x^{2} + 1 \lt 0 $”的否定是（B）
A.$ \forall x \in \mathbf{R},x^{2} + 1 \lt 0 $
B.$ \forall x \in \mathbf{R},x^{2} + 1 \geq 0 $
C.$ \exists x \in \mathbf{R},x^{2} + 1 \leq 0 $
D.$ \exists x \in \mathbf{R},x^{2} + 1 \geq 0 $

答案： 2. B 本题考查命题的否定 根据存在量词命题的否定是全称量词命题可得,命题:“$\exists x \in \mathbf { R } , x ^ { 2 } + 1 ＜ 0$”的否定是“$\forall x \in \mathbf { R } , x ^ { 2 } + 1 \geqslant 0$”. 故选 B.

3. 设 $ a,b $ 为实数，则“$ a - b \gt 0 $”是“$ a^{2} - b^{2} \gt 0 $”的（D）
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件

答案： 3. D 本题考查充分条件与必要条件 取 $a = 0 , b = - 1$,则 $a - b ＞ 0$,但 $a ^ { 2 } - b ^ { 2 } ＜ 0$,充分性不成立;取 $a = - 1 ,$$b = 0$,则 $a ^ { 2 } - b ^ { 2 } ＞ 0$,但 $a - b ＜ 0$,必要性不成立.故“$a -$$b ＞ 0$”是“$a ^ { 2 } - b ^ { 2 } ＞ 0$”的既不充分也不必要条件. 故选 D.

4. 若幂函数 $ f(x) = (a^{2} - 5a - 5)x^{a} $ 在 $ (0, + \infty) $ 上单调递增，则 $ a = $（6）
A.3
B.6
C.2
D.$ - 1 $

答案： 4. B 本题考查幂函数的性质 因为 $f ( x ) = ( a ^ { 2 } - 5 a -$5)$x ^ { a }$为幂函数，所以 $a ^ { 2 } - 5 a - 5 = 1$,解得 $a = 6$或 $a =$$- 1$,又因为 $f ( x )$在$( 0 , + \infty )$上单调递增，所以 $a ＞ 0$,因此 $a = 6$. 故选 B.

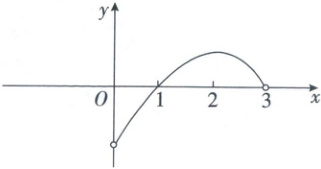
5. 已知 $ f(x) $ 是定义在 $ (-3,3) $ 上的奇函数，当 $ 0 \lt x \lt 3 $ 时 $ f(x) $ 的图象如图所示，那么不等式 $ f(x) \gt 0 $ 的解集是（C）

A.$ (1,3) $
B.$ (-3,-1) \cup (1,3) $
C.$ (-1,0) \cup (1,3) $
D.$ (-1,0) \cup (0,1) $

答案： 5. C 本题考查奇函数的图象 由题图可得,当 $x \in$$( 0 , 1 )$时$,f ( x ) ＜ 0$,当 $x \in ( 1 , 3 )$时$,f ( x ) ＞ 0$. 因为$f ( x )$是定义在$( - 3 , 3 )$上的奇函数，所以当 $x \in$$( - 1 , 0 )$时$,f ( x ) ＞ 0$,当 $x \in ( - 3 , - 1 )$时$,f ( x ) ＜ 0$,所以不等式 $f ( x ) ＞ 0$ 的解集是$( - 1 , 0 ) \cup ( 1 , 3 )$. 故选 C.

6. 我们知道，函数 $ y = f(x) $ 的图象关于坐标原点成中心对称图形的充要条件是函数 $ y = f(x) $ 为奇函数，有同学发现可以将其推广为：函数 $ y = f(x) $ 的图象关于点 $ P(a,b) $ 成中心对称图形的充要条件是函数 $ y = f(x + a) - b $ 为奇函数. 根据以上推广，则函数 $ f(x) = \frac{2x - 1}{x + 1} $ 图象的对称中心是（$(-1,2)$）
A.$ (-1,2) $
B.$ (-1,0) $
C.$ (1,2) $
D.$ (1,0) $

答案： 6. A 本题考查奇函数的性质 $f ( x ) = \frac { 2 x - 1 } { x + 1 }$,令$g ( x ) = f ( x + a ) - b$,则 $g ( x ) = \frac { 2 x + 2 a - 1 } { x + a + 1 } - b =$$\frac { 2 x + 2 a - 1 - b x - a b - b } { x + a + 1 }$为奇函数,定义域为$\{ x \mid x \neq$$- a - 1 \}$,且关于原点对称,故 $a = - 1 , g ( x ) =$$\frac { ( 2 - b ) x - 3 } { x }$ . 因为 $g ( x ) = - g ( - x )$,所以$\frac { ( 2 - b ) x - 3 } { x } =$$- \frac { ( 2 - b ) x - 3 } { - x }$,所以 $b = 2$,故函数$f ( x ) = \frac { 2 x - 1 } { x + 1 }$图象的对称中心为$( - 1 , 2 )$. 故选 A.

7. 从装满 10 升纯酒精的容器中倒出 2 升酒精，然后用水将容器加满，再倒出 2 升酒精溶液，再用水将容器加满，照这样的方法继续下去，设倒完第 $ k $ 次后，前 $ k $ 次共倒出纯酒精 $ x $ 升，倒完第 $ k + 1 $ 次后，前 $ k + 1 $ 次共倒出纯酒精 $ f(x) $ 升，则 $ f(x) $ 的解析式是（C）
A.$ f(x) = \frac{4}{5}(x + 2) $
B.$ f(x) = \frac{1}{5}x + 2 $
C.$ f(x) = \frac{4}{5}x + 2 $
D.$ f(x) = \frac{1}{5}x $

答案： 7. C 本题考查根据实际应用问题求函数解析式 因为第$k$次共倒出了纯酒精$x \mathrm { L }$,所以第$k$次倒出后容器中含纯酒精$( 1 0 - x ) \mathrm { L }$,则第$k + 1$次倒出了纯酒精$\frac { 1 0 - x } { 1 0 }$$· 2 \mathrm { L }$,所以倒完第$k + 1$次后,前$k + 1$次共倒出纯酒精的升数是$f ( x ) = x + \frac { 1 0 - x } { 1 0 } · 2 = \frac { 4 } { 5 } x + 2$. 故选 C.

8. 函数 $ f(x) = \frac{x^{3} - x}{x^{4} + x^{2} + 1} $ 在区间 $ [1,3] $ 上（A）
A.有最大值为 $ \frac{\sqrt{3}}{6} $，最小值为 0
B.有最大值为 $ \frac{24}{91} $，最小值为 0
C.有最大值为 $ \frac{\sqrt{3}}{6} $，无最小值
D.有最大值为 $ \frac{24}{91} $，无最小值

答案： 8. A 本题考查分式函数的化简及求最值 当$x \in [ 1 , 3 ]$时$,f ( x ) = \frac { x ^ { 3 } - x } { x ^ { 4 } + x ^ { 2 } + 1 } = \frac { x - \frac { 1 } { x } } { x ^ { 2 } + 1 + \frac { 1 } { x ^ { 2 } } } = \frac { x - \frac { 1 } { x } } { ( x - \frac { 1 } { x } ) ^ { 2 } + 3 }$. 设$x - \frac { 1 } { x } = t$,易知$t = x - \frac { 1 } { x }$在$[ 1 , 3 ]$上单调递增,所以$t \in [ 0 , \frac { 8 } { 3 } ]$. 令$g ( t ) = \frac { t } { t ^ { 2 } + 3 }$,则$g ( 0 ) = 0$,当$t ＞ 0$时,$g ( t ) = \frac { 1 } { t + \frac { 3 } { t } }$,函数$y = x + \frac { 3 } { x }$在$( 0 , \sqrt { 3 } )$上单调递减,在$( \sqrt { 3 } , \frac { 8 } { 3 } ]$上单调递增,且$y ＞ 0$,故$g ( t ) _ { \max } =$$g ( \sqrt { 3 } ) = \frac { \sqrt { 3 } } { 6 } , g ( t ) _ { \min } ＞ 0$. 综上所述,$g ( t ) _ { \max } = \frac { \sqrt { 3 } } { 6 } ,$$g ( t ) _ { \min } = 0$,即$f ( x ) _ { \max } = \frac { \sqrt { 3 } } { 6 } , f ( x ) _ { \min } = 0$. 故选 A.