《2025年期中期末名校名区真题精编高一数学上册人教版》

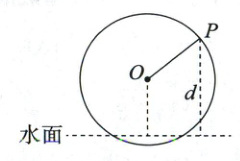
16. （15 分）如图，一个半径为 $ 3 \mathrm { m } $ 的筒车按逆时针方向每分转 $ 1.5 $ 圈，筒车的轴心 $ O $ 距离水面的高度为 $ \frac { 3 \sqrt { 2 } } { 2 } \mathrm { m } $.设筒车上的某个盛水筒 $ P $ 到水面的距离为 $ d $（单位：$ \mathrm { m } $）（在水面下则 $ d $ 为负数），若以盛水筒 $ P $ 刚浮出水面时开始计算时间，则 $ d $ 与时间 $ t $（单位：$ \mathrm { s } $）之间的关系为 $ d = A \sin ( \omega t + \varphi ) + K \left( A ＞ 0, \omega ＞ 0, - \frac { \pi } { 2 } ＜ \varphi ＜ \frac { \pi } { 2 } \right) $.
（1）求 $ A $，$ \omega $，$ \varphi $，$ K $ 的值；
（2）盛水筒出水后至少经过多长时间就可到达最高点？

答案： 16.[解析] 本题考查三角函数的实际应用
(1)依题意，$d = A\sin(\omega t+\varphi)+\frac {3\sqrt{2}}{2}$，因为筒车的半径为$3m$，所以振幅$A = 3$，筒车按逆时针方向每分转$1.5$圈，故角速度为$\omega=\frac {1.5×2\pi}{60}=\frac {\pi}{20}$，因为以筒车上盛水筒$P$刚浮出水面时开始计时，所以$3\sin(\frac {\pi}{20}×0+\varphi)+\frac {3\sqrt{2}}{2}=0$，且$-\frac {\pi}{2}＜\varphi＜\frac {\pi}{2}$，解得$\varphi=-\frac {\pi}{4}$，所以$d = 3\sin(\frac {\pi}{20}t-\frac {\pi}{4})+\frac {3\sqrt{2}}{2}$。综上，$A = 3$，$\omega=\frac {\pi}{20}$，$\varphi=-\frac {\pi}{4}$，$K=\frac {3\sqrt{2}}{2}$。
(2)根据题意，令$\frac {\pi}{20}t-\frac {\pi}{4}=\frac {\pi}{2}$，可得$t = 15$。所以盛水筒出水后至少经过$15s$就可到达最高点。

17. （15 分）已知函数 $ f ( x ) = \sin \omega x - \sqrt { 3 } \cos \omega x ( \omega ＞ 0 ) $ 的最小正周期为 $ \pi $.
（1）求函数 $ f ( x ) $ 的单调递增区间；
（2）设 $ x \in ( - \pi, \pi ) $，求不等式 $ f ( x ) \geq 1 $ 的解集.

答案： 17.[解析] 本题考查三角恒等变换、三角函数的性质
(1)函数$f(x)=\sin\omega x-\sqrt{3}\cos\omega x = 2\sin(\omega x-\frac {\pi}{3})$，因为$\omega＞0$，$f(x)$的最小正周期为$\frac {2\pi}{\omega}=\pi$，所以$\omega = 2$，所以$f(x)=2\sin(2x-\frac {\pi}{3})$。令$-\frac {\pi}{2}+2k\pi\leq2x-\frac {\pi}{3}\leq\frac {\pi}{2}+2k\pi$，$k\in Z$，解得$-\frac {\pi}{12}+k\pi\leq x\leq\frac {5\pi}{12}+k\pi$，$k\in Z$，所以函数$f(x)$的单调递增区间为$[-\frac {\pi}{12}+k\pi,\frac {5\pi}{12}+k\pi](k\in Z)$。
(2)因为$f(x)\geq1$，所以$\sin(2x-\frac {\pi}{3})\geq\frac {1}{2}$，所以$\frac {\pi}{6}+2k_1\pi\leq2x-\frac {\pi}{3}\leq\frac {5\pi}{6}+2k_1\pi$，$k_1\in Z$，解得$\frac {\pi}{4}+k_1\pi\leq x\leq\frac {7\pi}{12}+k_1\pi$，$k_1\in Z$，因为$x\in(-\pi,\pi)$，当$k_1 = - 1$时，$x\in[-\frac {3\pi}{4},-\frac {5\pi}{12}]$，当$k_1 = 0$时，$x\in[\frac {\pi}{4},\frac {7\pi}{12}]$，所以原不等式的解集为$\{x|-\frac {3\pi}{4}\leq x\leq-\frac {5\pi}{12}$或$\frac {\pi}{4}\leq x\leq\frac {7\pi}{12}\}$。