《2025年期中期末名校名区真题精编高一数学上册人教版》

16. （15 分）如图，在平面直角坐标系 $ xOy $ 中，角 $ \theta $ 的终边与单位圆交于点 $ P $.
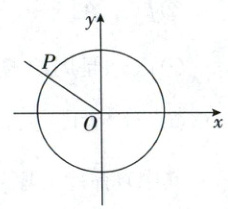
（1）若图中点 $ P $ 的横坐标为 $ -\frac{3}{5} $，求 $ \cos 2\theta - \sin \theta · \cos \theta $ 的值；
（2）若将 $ OP $ 绕点 $ O $ 逆时针旋转 $ \frac{\pi}{4} $，得到角 $ \alpha $（即 $ \alpha = \theta + \frac{\pi}{4} $），若 $ \tan \alpha = \frac{1}{2} $，求 $ \tan \theta $ 的值.

答案： 16.[解析]　本题考查三角函数的定义、三角恒等变换
(1)因为点P在单位圆上，且点P的横坐标为−$\frac{3}{5}$，所以cosθ=−$\frac{3}{5}$，sinθ=$\frac{4}{5}$，所以cos2θ−sinθ·cosθ=1−2sin²θ−sinθ·cosθ=1−2×$\frac{16}{25}$−$\frac{4}{5}$×(−$\frac{3}{5}$)=$\frac{1}{5}$.
(2)由题知α=θ+$\frac{π}{4}$，则θ=α−$\frac{π}{4}$，则tanθ=tan(α−$\frac{π}{4}$)=$\frac{tanα - tan\frac{π}{4}}{1 + tanα·tan\frac{π}{4}}$=$\frac{\frac{1}{2} - 1}{1 + \frac{1}{2}}$=$\frac{-\frac{1}{2}}{\frac{3}{2}}$=−$\frac{1}{3}$.

17. （15 分）某工厂利用辐射对食品进行灭菌消毒，先准备在该厂附近建一职工宿舍，并对宿舍进行防辐射处理，防辐射材料的选用与宿舍到工厂的距离有关. 若建造宿舍的所有费用 $ p $（单位：万元）和宿舍到工厂的距离 $ x $（单位：$ km $）的关系式为 $ p = \frac{k}{4x + 5}(0 \leq x \leq 15) $，若距离为 $ 10 km $ 时，测算宿舍建造费用为 20 万元. 为了交通方便，工厂与宿舍之间还要修一条道路，已知购置修路设备需 10 万元，铺设路面每千米成本为 4 万元. 设 $ f(x) $ 为建造宿舍与修路费用之和.
（1）求 $ f(x) $ 的表达式；
（2）宿舍建在离工厂多远处，可使总费用最少？并求 $ f(x) $ 的最小值.

答案： 17.[解析]　本题考查函数的实际应用、利用基本不等式求最值
(1)由距离为10 km时，测算宿舍建造费用为20万元，得20 = $\frac{k}{4 × 10 + 5}$，解得k = 900，所以p = $\frac{900}{4x + 5}$，则f(x) = $\frac{900}{4x + 5} + 10 + 4x$，0 ≤ x ≤ 15.
(2)因为f(x) = $\frac{900}{4x + 5} + 10 + 4x$ = $\frac{900}{4x + 5} + (4x + 5) + 5$ ≥ 2$\sqrt{\frac{900}{4x + 5} · (4x + 5)}$ + 5 = 65，当且仅当$\frac{900}{4x + 5} = 4x + 5$，即x = $\frac{25}{4}$时取等号，此时总费用最少. 故宿舍建在离工厂$\frac{25}{4}$ km处，可使总费用最少，f(x)的最小值为65.