《2025年期中期末名校名区真题精编高一数学上册人教版》

1. 如图，在△ABC中，H为BC的中点，M为AH的中点，若$\overrightarrow{AM}=\lambda\overrightarrow{AB}+\mu\overrightarrow{AC}$，则$\lambda+\mu=$（B）

A.$\frac{2}{3}$
B.$\frac{1}{2}$
C.$\frac{1}{6}$
D.$\frac{1}{3}$

答案： 1.B 本题考查平面向量的线性运算 在△ABC 中,H 为BC 的中点,M 为AH 的中点,则$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AH}=\frac{1}{2}×\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,所以λ=μ=$\frac{1}{4}$,所以λ+μ=$\frac{1}{2}$.故选B.

2. 甲、乙两个跑步爱好者记录了去年下半年每个月的跑步里程（单位：千米），现将两人的数据绘制成如图所示的折线图，则下列结论中正确的是（D）

A.甲跑步里程的极差是120
B.乙跑步里程的中位数是270
C.分别记甲、乙去年下半年每月跑步里程的平均数为$m_1$，$m_2$，则$m_1＞m_2$
D.分别记甲、乙去年下半年每月跑步里程的标准差为$s_1$，$s_2$，则$s_1＞s_2$

答案： 2.D 本题考查统计数据的计算与辨析 对于A,甲跑步里程的极差为313 - 203 = 110,A错误;对于B,乙跑步里程的中位数为$\frac{280 + 266}{2}$ = 273,B错误;对于C,甲去年下半年每月跑步里程的平均数为$\frac{313 + 254 + 217 + 245 + 203 + 301}{6}$ = 255.5,乙去年下半年每月跑步里程的平均数为$\frac{293 + 280 + 262 + 283 + 255 + 266}{6}$≈273.2,m₁＜m₂,C错误;对于D,由题图知,甲的跑步里程数据波动大,乙的跑步里程数据波动小,故s₁＞s₂,D正确.故选D.

3. 幂函数$f(x)=(m^2 - m - 1)x^{m^2 + m - 3}$在$(0,+\infty)$上是减函数，则实数$m$的值为（B）
A.2或-1
B.-1
C.2
D.-2或-1

答案： 3.B 本题考查幂函数的定义及单调性 由题意可知,m² - m - 1 = 1,解得m = -1或m = 2,当m = -1时,f(x) = x⁻³,函数在(0,+∞)上是减函数,符合题意,当m = 2时,f(x) = x³,函数在(0,+∞)上是增函数,不符合题意,所以m = -1.故选B.

4. 已知$a=\ln\frac{1}{2}$，$b=2^{1.2}$，$c=\log_35$，则$a$，$b$，$c$的大小关系为（C）
A.$c＞a＞b$
B.$b＞a＞c$
C.$b＞c＞a$
D.$c＞b＞a$

答案： 4.C 本题考查指数、对数的大小比较 b = 2¹.²＞2 = log₃9＞c = log₃5＞1＞0＞a = ln$\frac{1}{2}$,即b＞c＞a.故选C.

5. 已知函数$f(x + 1)$是偶函数，当$1＜x_1＜x_2$时，$[f(x_1) - f(x_2)](x_1 - x_2)＞0$恒成立，设$a = f(-\frac{1}{2})$，$b = f(2)$，$c = f(3)$，则$a$，$b$，$c$的大小关系为（B）
A.$c ＜ b ＜ a$
B.$b ＜ a ＜ c$
C.$b ＜ c ＜ a$
D.$a ＜ b ＜ c$

答案： 5.B 本题考查利用函数的单调性和奇偶性比较大小
思路探寻
f(x + 1)是偶函数→函数f(x)图象的对称轴为直线x = 1,f(-$\frac{1}{2}$) = f($\frac{5}{2}$)→即可判断选项.
当1＜x₁＜x₂时,[f(x₁) - f(x₂)](x₁ - x₂)＞0恒成立→函数f(x)在(1,+∞)上单调递增
因为当1＜x₁＜x₂时,[f(x₁) - f(x₂)](x₁ - x₂)＞0恒成立,所以当1＜x₁＜x₂时,f(x₂) - f(x₁)＞0,即f(x₂)＞f(x₁),所以函数f(x)在(1,+∞)上单调递增.
因为函数f(x + 1)是偶函数,即f(1 + x) = f(1 - x),所以函数f(x)的图象关于直线x = 1对称,所以a = f(-$\frac{1}{2}$) = f($\frac{5}{2}$).
又函数f(x)在(1,+∞)上单调递增,所以f
(2)＜f($\frac{5}{2}$)＜f
(3),即f
(2)＜f(-$\frac{1}{2}$)＜f
(3),所以b＜a＜c.故选B.
一题多解
已知函数f(x + 1)是偶函数,当1＜x₁＜x₂时,[f(x₁) - f(x₂)](x₁ - x₂)＞0恒成立,故函数f(x) = (x - 1)²符合要求,把x = -$\frac{1}{2}$,x = 2,x = 3分别代入f(x) = (x - 1)²即可得b＜a＜c,故选B.

6. 若函数$f(x)=\lg(x^2 - ax + 3a)$在区间$(2,+\infty)$上单调递增，则$a$的取值范围为（D）
A.$(-\infty,4)$
B.$(-\infty,4]$
C.$[-4,4)$
D.$[-4,4]$

答案： 6.D 本题考查利用复合函数的单调性求参数的取值范围
思路探寻
f(x) = lg(x² - ax + 3a)在区间(2,+∞)上单调递增
y = x² - ax + 3a在区间(2,+∞)上单调递增
y = lgx单调递增
由复合函数单调性可知y = x² - ax + 3a在区间(2,+∞)上单调递增,所以$\frac{a}{2}$≤2且2² - 2a + 3a≥0→即可得解.
易知y = lgx在区间(2,+∞)上单调递增,由复合函数单调性可知y = x² - ax + 3a在区间(2,+∞)上单调递增,所以$\frac{a}{2}$≤2且2² - 2a + 3a≥0,解得 - 4≤a≤4.
综上可知,a的取值范围为[-4,4].故选D.
易错提醒
本题容易忽视函数的定义域,即2² - 2a + 3a≥0必须成立这个条件导致错误.

7. 已知4个数据的平均数为6，方差为3，现又加入一个数据6，此时这5个数据的方差为（$\frac{12}{5}$）
A.$\frac{24}{5}$
B.$\frac{16}{5}$
C.$\frac{14}{5}$
D.$\frac{12}{5}$

答案： 7.D 本题考查平均数与方差 因为4个数据的平均数为6,方差为3,所以$\frac{1}{4}$$\sum_{i = 1}^{4}$(xᵢ - 6)² = 3(其中四个数为xᵢ,i = 1,2,3,4),故$\sum_{i = 1}^{4}$(xᵢ - 6)² = 12.
加入一个数据6后,5个数的平均数还是6,则方差为$\frac{1}{5}$[$\sum_{i = 1}^{4}$(xᵢ - 6)² + (6 - 6)²] = $\frac{12 + 0}{5}$ = $\frac{12}{5}$,即这5个数据的方差为$\frac{12}{5}$.故选D.

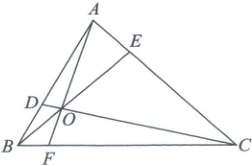
8. 如图，已知$D$，$E$分别是△ABC边$AB$，$AC$上的点，且满足$\overrightarrow{AB}=\frac{3}{2}\overrightarrow{AD}$，$\overrightarrow{AC}=4\overrightarrow{AE}$，$BE$与$CD$交于点$O$，连接$AO$并延长交$BC$于点$F$.若$\overrightarrow{AO}=\lambda\overrightarrow{OF}$，则实数$\lambda$的值为（A）

A.$\frac{7}{3}$
B.$\frac{4}{3}$
C.$\frac{5}{2}$
D.2

答案： 8.A 本题考查平面向量基本定理和向量共线定理的综合运用
思路探寻
D,O,C三点共线,B,O,E三点共线
$\overrightarrow{DO}$ = k$\overrightarrow{DC}$ = k($\overrightarrow{AC}$ - $\frac{2}{3}$$\overrightarrow{AB}$),k∈R
$\overrightarrow{BO}$ = μ$\overrightarrow{BE}$ = μ($\frac{1}{4}$$\overrightarrow{AC}$ - $\overrightarrow{AB}$),μ∈R
$\overrightarrow{AO}$ = $\frac{2}{3}$(1 - k)$\overrightarrow{AB}$ + k$\overrightarrow{AC}$,
$\overrightarrow{AO}$ = (1 - μ)$\overrightarrow{AB}$ + $\frac{μ}{4}$$\overrightarrow{AC}$
$\overrightarrow{AO}$ = λ$\overrightarrow{OF}$
$\overrightarrow{AO}$ = $\frac{3}{5}$$\overrightarrow{AB}$ + $\frac{1}{10}$$\overrightarrow{AC}$← 求出参数k,μ←
$\overrightarrow{AF}$ = $\frac{λ + 1}{λ}$$\overrightarrow{AO}$ = $\frac{3λ + 3}{5λ}$$\overrightarrow{AB}$ + $\frac{λ + 1}{10λ}$$\overrightarrow{AC}$
因为B,F,C三点共线,所以$\frac{3λ + 3}{5λ}$ + $\frac{λ + 1}{10λ}$ = 1,解得λ = $\frac{7}{3}$.故选A.