2025年期中期末名校名区真题精编高一数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年期中期末名校名区真题精编高一数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 已知$f(x)$是定义在$R$上的偶函数,且在区间$[0,+\infty)$上单调递减,则不等式$f(2x - 1)>f(x + 1)$的解集为(
A.$(0,2)$
B.$(-\infty,0)\cup(2,+\infty)$
C.$(-\infty,2)$
D.$(2,+\infty)$
A
)A.$(0,2)$
B.$(-\infty,0)\cup(2,+\infty)$
C.$(-\infty,2)$
D.$(2,+\infty)$
答案:
7.A 本题考查利用函数性质解不等式 因为$f(x)$是定义在$\mathbf{R}$上的偶函数,且在区间$[0,+\infty)$上单调递减,所以$f(2x - 1)>f(x + 1)\Leftrightarrow(2x - 1)^2<(x + 1)^2$,即$4x^2 - 4x + 1<x^2 + 2x + 1$,整理得$x(x - 2)<0$,解得$x\in(0,2)$.故选A.
8. 若关于$x$的方程$(\sin x+\cos x)^{2}+\cos2x = m$在区间$(0,\pi]$上有两个不同的实数根$x_{1},x_{2}$,且$\vert x_{1}-x_{2}\vert\geq\frac{\pi}{4}$,则实数$m$的取值范围是( )
A.$[0,2)$
B.$[0,2]$
C.$[1,\sqrt{2}+1]$
D.$[1,\sqrt{2}+1)$
A.$[0,2)$
B.$[0,2]$
C.$[1,\sqrt{2}+1]$
D.$[1,\sqrt{2}+1)$
答案:
8.B 本题考查利用三角函数的图象研究方程根的问题
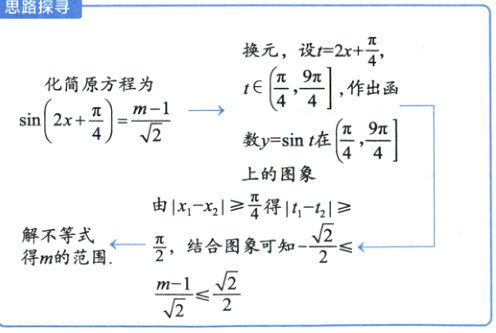
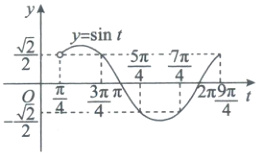
化简原方程为$\sin(2x+\frac{\pi}{4})=\frac{m - 1}{\sqrt{2}}\rightarrow$换元,设$t = 2x+\frac{\pi}{4}$,$t\in(\frac{\pi}{4},\frac{9\pi}{4}]$,作出函数$y = \sin t$在$(\frac{\pi}{4},\frac{9\pi}{4}]$上的图象
由$\vert x_1 - x_2\vert\geq\frac{\pi}{4}$得$\vert t_1 - t_2\vert\geq\frac{\pi}{2}$,所以$-\frac{\sqrt{2}}{2}\leq\frac{m - 1}{\sqrt{2}}\leq\frac{\sqrt{2}}{2}$,故$0\leq m\leq2$.故选B.
名师点拨
对于根据含三角函数的方程的实数根个数求参数取值范围问题,常用的解题策略是数形结合,即结合三角函数图象将问题转化为不等式的解集问题.
8.B 本题考查利用三角函数的图象研究方程根的问题

化简原方程为$\sin(2x+\frac{\pi}{4})=\frac{m - 1}{\sqrt{2}}\rightarrow$换元,设$t = 2x+\frac{\pi}{4}$,$t\in(\frac{\pi}{4},\frac{9\pi}{4}]$,作出函数$y = \sin t$在$(\frac{\pi}{4},\frac{9\pi}{4}]$上的图象
由$\vert x_1 - x_2\vert\geq\frac{\pi}{4}$得$\vert t_1 - t_2\vert\geq\frac{\pi}{2}$,所以$-\frac{\sqrt{2}}{2}\leq\frac{m - 1}{\sqrt{2}}\leq\frac{\sqrt{2}}{2}$,故$0\leq m\leq2$.故选B.

名师点拨
对于根据含三角函数的方程的实数根个数求参数取值范围问题,常用的解题策略是数形结合,即结合三角函数图象将问题转化为不等式的解集问题.
9. 已知$\theta\in(0,\pi)$,$\sin\theta+\cos\theta=\frac{1}{5}$,则下列结论正确的是(
A.$\theta\in(\frac{\pi}{2},\pi)$
B.$\cos\theta=-\frac{3}{5}$
C.$\tan\theta=-\frac{3}{4}$
D.$\sin\theta-\cos\theta=\frac{7}{5}$
ABD
)A.$\theta\in(\frac{\pi}{2},\pi)$
B.$\cos\theta=-\frac{3}{5}$
C.$\tan\theta=-\frac{3}{4}$
D.$\sin\theta-\cos\theta=\frac{7}{5}$
答案:
9.ABD 本题考查同角三角函数的基本关系 将$\sin\theta+\cos\theta=\frac{1}{5}$两边同时平方可得,$\sin^2\theta+2\sin\theta\cos\theta+\cos^2\theta=1+2\sin\theta\cos\theta=\frac{1}{25}$,则$2\sin\theta\cos\theta=-\frac{24}{25}$,又$\theta\in(0,\pi)$,所以$\sin\theta>0$,$\cos\theta<0$,所以$\theta\in(\frac{\pi}{2},\pi)$,所以A正确;
又由$(\sin\theta-\cos\theta)^2=\sin^2\theta-2\sin\theta\cos\theta+\cos^2\theta=\frac{49}{25}$,得$\sin\theta-\cos\theta=\frac{7}{5}$,所以D正确;
联立方程$\begin{cases}\sin\theta+\cos\theta=\frac{1}{5},\\\sin\theta-\cos\theta=\frac{7}{5},\end{cases}$解得$\begin{cases}\sin\theta=\frac{4}{5},\\\cos\theta=-\frac{3}{5},\end{cases}$所以B正确;
由同角三角函数的基本关系,可得$\tan\theta=\frac{\sin\theta}{\cos\theta}=-\frac{4}{3}$,所以C错误.故选ABD.
又由$(\sin\theta-\cos\theta)^2=\sin^2\theta-2\sin\theta\cos\theta+\cos^2\theta=\frac{49}{25}$,得$\sin\theta-\cos\theta=\frac{7}{5}$,所以D正确;
联立方程$\begin{cases}\sin\theta+\cos\theta=\frac{1}{5},\\\sin\theta-\cos\theta=\frac{7}{5},\end{cases}$解得$\begin{cases}\sin\theta=\frac{4}{5},\\\cos\theta=-\frac{3}{5},\end{cases}$所以B正确;
由同角三角函数的基本关系,可得$\tan\theta=\frac{\sin\theta}{\cos\theta}=-\frac{4}{3}$,所以C错误.故选ABD.
10. 若$a>b>1$,$x=\log_{a}b$,$y=\log_{b}a$,$z=a^{b}$,则下列结论一定正确的是(
A.$x<y$
B.$y<z$
C.$x<z$
D.$y>z$
AC
)A.$x<y$
B.$y<z$
C.$x<z$
D.$y>z$
答案:
10.AC 本题考查指数、对数比较大小 由$a>b>1$,得$0=\log_a1<\log_ab<\log_aa=1$,即$0<x<1$.$y=\log_ba$,即$y=\frac{1}{x}$,则$y=\frac{1}{x}>1$,所以$y>x$,故A正确.$z=a^b>a^1=a>1$,所以$z>x$,故C正确.
取$a = 2,b = \sqrt{2}$,满足$a>b>1$,则$y=\log_{\sqrt{2}}2 = 2$,$z=2^{\sqrt{2}}>2^1 = 2$,此时$z>y$;取$a = 2,b = 2^{\frac{1}{4}}$,满足$a>b>1$,则$y=\log_{2^{\frac{1}{4}}}2 = 4$,$z=2^{2^{\frac{1}{4}}}<2^2 = 4$,此时$z<y$,所以$z,y$的大小关系不确定.故选AC.
取$a = 2,b = \sqrt{2}$,满足$a>b>1$,则$y=\log_{\sqrt{2}}2 = 2$,$z=2^{\sqrt{2}}>2^1 = 2$,此时$z>y$;取$a = 2,b = 2^{\frac{1}{4}}$,满足$a>b>1$,则$y=\log_{2^{\frac{1}{4}}}2 = 4$,$z=2^{2^{\frac{1}{4}}}<2^2 = 4$,此时$z<y$,所以$z,y$的大小关系不确定.故选AC.
11. 已知函数$f(x)=1 + 2\cos x\cos(x + 2\varphi)$是偶函数,其中$\varphi\in(0,\pi)$,则下列关于函数$g(x)=\cos(2x-\varphi)$的描述中正确的是(
A.$g(x)$在区间$[-\frac{\pi}{12},\frac{\pi}{3}]$上的最小值为$-\frac{1}{2}$
B.$g(x)$的图象可由函数$f(x)$的图象向左平移$\frac{\pi}{4}$个单位长度得到
C.点$(\frac{\pi}{4},0)$是$g(x)$的图象的一个对称中心
D.$[0,\frac{\pi}{2}]$是$g(x)$的一个单调递增区间
AB
)A.$g(x)$在区间$[-\frac{\pi}{12},\frac{\pi}{3}]$上的最小值为$-\frac{1}{2}$
B.$g(x)$的图象可由函数$f(x)$的图象向左平移$\frac{\pi}{4}$个单位长度得到
C.点$(\frac{\pi}{4},0)$是$g(x)$的图象的一个对称中心
D.$[0,\frac{\pi}{2}]$是$g(x)$的一个单调递增区间
答案:
11.AB 本题考查三角函数的图象与性质 由$f(-x)=f(x)$得$2\cos(-x)\cos(-x + 2\varphi)=2\cos x\cos(x + 2\varphi)$,所以$\cos(-x + 2\varphi)=\cos(x + 2\varphi)$恒成立,所以直线$x = 2\varphi$是曲线$y=\cos x$的对称轴,所以$2\varphi=k\pi(k\in\mathbf{Z})$,即$\varphi=\frac{k\pi}{2}(k\in\mathbf{Z})$,又$\varphi\in(0,\pi)$,所以$\varphi=\frac{\pi}{2}$,则$g(x)=\cos(2x - \frac{\pi}{2})=\sin2x$.
对于A,因为$x\in[-\frac{\pi}{12},\frac{\pi}{3}]$,所以$2x\in[-\frac{\pi}{6},\frac{2\pi}{3}]$,所以$g(x)$在区间$[-\frac{\pi}{12},\frac{\pi}{3}]$上的最小值为$g(-\frac{\pi}{12})=-\frac{1}{2}$,故A正确;
对于B,$f(x)=1 + 2\cos x\cos(x + \pi)=1 - 2\cos^2x=-\cos2x$,将函数$f(x)$的图象向左平移$\frac{\pi}{4}$个单位长度,得到函数$y=-\cos2(x + \frac{\pi}{4})=\sin2x=g(x)$的图象,故B正确;
对于C,$g(\frac{\pi}{4})=\sin\frac{\pi}{2}=1$,所以点$(\frac{\pi}{4},0)$不是$g(x)$的图象的一个对称中心,故C错误;
对于D,当$x\in[0,\frac{\pi}{2}]$时,$2x\in[0,\pi]$,此时$g(x)$先单调递增,再单调递减,所以$[0,\frac{\pi}{2}]$不是$g(x)$的一个单调递增区间,故D错误.故选AB.
名师点拨
本题的解题关键是由函数$f(x)=1 + 2\cos x\cos(x + 2\varphi)$是偶函数求出参数$\varphi$的值,具体方法是利用$f(-x)=f(x)$恒成立得到$\cos(-x + 2\varphi)=\cos(x + 2\varphi)$恒成立,从而得出$\varphi$的值.
对于A,因为$x\in[-\frac{\pi}{12},\frac{\pi}{3}]$,所以$2x\in[-\frac{\pi}{6},\frac{2\pi}{3}]$,所以$g(x)$在区间$[-\frac{\pi}{12},\frac{\pi}{3}]$上的最小值为$g(-\frac{\pi}{12})=-\frac{1}{2}$,故A正确;
对于B,$f(x)=1 + 2\cos x\cos(x + \pi)=1 - 2\cos^2x=-\cos2x$,将函数$f(x)$的图象向左平移$\frac{\pi}{4}$个单位长度,得到函数$y=-\cos2(x + \frac{\pi}{4})=\sin2x=g(x)$的图象,故B正确;
对于C,$g(\frac{\pi}{4})=\sin\frac{\pi}{2}=1$,所以点$(\frac{\pi}{4},0)$不是$g(x)$的图象的一个对称中心,故C错误;
对于D,当$x\in[0,\frac{\pi}{2}]$时,$2x\in[0,\pi]$,此时$g(x)$先单调递增,再单调递减,所以$[0,\frac{\pi}{2}]$不是$g(x)$的一个单调递增区间,故D错误.故选AB.
名师点拨
本题的解题关键是由函数$f(x)=1 + 2\cos x\cos(x + 2\varphi)$是偶函数求出参数$\varphi$的值,具体方法是利用$f(-x)=f(x)$恒成立得到$\cos(-x + 2\varphi)=\cos(x + 2\varphi)$恒成立,从而得出$\varphi$的值.
12. 设$m,n\in R_{+}$,且$m + n = 1$,则$\frac{1}{n}+\frac{4}{m}$的最小值为
9
.
答案:
12.9 [解析] 本题考查利用基本不等式求最值
$\frac{1}{n}+\frac{4}{m}=(\frac{1}{n}+\frac{4}{m})(m + n)=\frac{m}{n}+1 + 4+\frac{4n}{m}=5+\frac{m}{n}+\frac{4n}{m}=5 + 2\sqrt{\frac{m}{n}·\frac{4n}{m}}=9$,
当且仅当$\begin{cases}\frac{m}{n}=\frac{4n}{m},\\m + n = 1,\end{cases}$即$\begin{cases}m=\frac{2}{3},\\n=\frac{1}{3}\end{cases}$时取等号.故$\frac{1}{n}+\frac{4}{m}$的最小值为9.
$\frac{1}{n}+\frac{4}{m}=(\frac{1}{n}+\frac{4}{m})(m + n)=\frac{m}{n}+1 + 4+\frac{4n}{m}=5+\frac{m}{n}+\frac{4n}{m}=5 + 2\sqrt{\frac{m}{n}·\frac{4n}{m}}=9$,
当且仅当$\begin{cases}\frac{m}{n}=\frac{4n}{m},\\m + n = 1,\end{cases}$即$\begin{cases}m=\frac{2}{3},\\n=\frac{1}{3}\end{cases}$时取等号.故$\frac{1}{n}+\frac{4}{m}$的最小值为9.
13. 已知函数$f(x)=2\sin\omega x\cos^{2}(\frac{\omega x}{2}-\frac{\pi}{4})-\sin^{2}\omega x(\omega>0)$,现将该函数图象先向左平移$\frac{\pi}{3\omega}$个单位长度,再将图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,得到函数$g(x)$的图象,已知函数$g(x)$在区间$(\frac{\pi}{2},\pi)$上是单调的,则$\omega$的取值范围是
$(0,\frac{1}{12}]∪[\frac{1}{6},\frac{7}{12}]$
.
答案:
13.$(0,\frac{1}{12}]∪[\frac{1}{6},\frac{7}{12}]$ [解析] 本题考查三角函数的图象与性质 $f(x)=2\sin\omega x\cos^2(\frac{\omega x}{2}-\frac{\pi}{4})-\sin^2\omega x=\sin\omega x(1+\sin\omega x)-\sin^2\omega x=\sin\omega x$.
依题意,$g(x)=f(2x+\frac{\pi}{3})=\sin(2\omega x+\frac{\pi}{3})$,
当$x\in(\frac{\pi}{2},\pi)$时,
由$\omega>0$得$2\omega x+\frac{\pi}{3}\in(\omega\pi+\frac{\pi}{3},2\omega\pi+\frac{\pi}{3})$,
又$g(x)$在$(\frac{\pi}{2},\pi)$上单调,
所以$(\omega\pi+\frac{\pi}{3},2\omega\pi+\frac{\pi}{3})\subseteq(\frac{\pi}{3},\frac{\pi}{2})$,
或$(\omega\pi+\frac{\pi}{3},2\omega\pi+\frac{\pi}{3})\subseteq(\frac{\pi}{2}+k\pi,\frac{3\pi}{2}+k\pi)(k\in\mathbf{N})$,
所以$\begin{cases}\omega\pi+\frac{\pi}{3}>\frac{\pi}{3},\\2\omega\pi+\frac{\pi}{3}\leq\frac{\pi}{2},\end{cases}$解得$0<\omega\leq\frac{1}{12}$;
$\begin{cases}\omega\pi+\frac{\pi}{3}\geq\frac{\pi}{2}+k\pi,\\2\omega\pi+\frac{\pi}{3}\leq\frac{3\pi}{2}+k\pi,\end{cases}$解得$\frac{1}{6}+k\leq\omega\leq\frac{7}{12}+\frac{k}{2}(k\in\mathbf{N})$,
由$\frac{7}{12}+\frac{k}{2}>\frac{1}{6}+k$,解得$k<\frac{5}{6}$,又$k\in\mathbf{N}$,所以$k = 0$,
所以$\omega\in[\frac{1}{6},\frac{7}{12}]$.
综上,$\omega$的取值范围为$(0,\frac{1}{12}]∪[\frac{1}{6},\frac{7}{12}]$.
依题意,$g(x)=f(2x+\frac{\pi}{3})=\sin(2\omega x+\frac{\pi}{3})$,
当$x\in(\frac{\pi}{2},\pi)$时,
由$\omega>0$得$2\omega x+\frac{\pi}{3}\in(\omega\pi+\frac{\pi}{3},2\omega\pi+\frac{\pi}{3})$,
又$g(x)$在$(\frac{\pi}{2},\pi)$上单调,
所以$(\omega\pi+\frac{\pi}{3},2\omega\pi+\frac{\pi}{3})\subseteq(\frac{\pi}{3},\frac{\pi}{2})$,
或$(\omega\pi+\frac{\pi}{3},2\omega\pi+\frac{\pi}{3})\subseteq(\frac{\pi}{2}+k\pi,\frac{3\pi}{2}+k\pi)(k\in\mathbf{N})$,
所以$\begin{cases}\omega\pi+\frac{\pi}{3}>\frac{\pi}{3},\\2\omega\pi+\frac{\pi}{3}\leq\frac{\pi}{2},\end{cases}$解得$0<\omega\leq\frac{1}{12}$;
$\begin{cases}\omega\pi+\frac{\pi}{3}\geq\frac{\pi}{2}+k\pi,\\2\omega\pi+\frac{\pi}{3}\leq\frac{3\pi}{2}+k\pi,\end{cases}$解得$\frac{1}{6}+k\leq\omega\leq\frac{7}{12}+\frac{k}{2}(k\in\mathbf{N})$,
由$\frac{7}{12}+\frac{k}{2}>\frac{1}{6}+k$,解得$k<\frac{5}{6}$,又$k\in\mathbf{N}$,所以$k = 0$,
所以$\omega\in[\frac{1}{6},\frac{7}{12}]$.
综上,$\omega$的取值范围为$(0,\frac{1}{12}]∪[\frac{1}{6},\frac{7}{12}]$.
14. 已知函数$f(x)=\begin{cases}ax + 1,x\leq0,\\\vert\ln x\vert,x>0,\end{cases}$给出下列三个结论:
①当$a = - 2$时,函数$f(x)$的单调递减区间为$(-\infty,1)$;
②若函数$f(x)$无最小值,则$a$的取值范围为$(0,+\infty)$;
③若$a<1$且$a\neq0$,则$\exists b\in R$,使得函数$y = f(x)-b$恰有3个零点$x_{1},x_{2},x_{3}$,且$x_{1}x_{2}x_{3}=-1$.其中,所有正确结论的序号是______.
①当$a = - 2$时,函数$f(x)$的单调递减区间为$(-\infty,1)$;
②若函数$f(x)$无最小值,则$a$的取值范围为$(0,+\infty)$;
③若$a<1$且$a\neq0$,则$\exists b\in R$,使得函数$y = f(x)-b$恰有3个零点$x_{1},x_{2},x_{3}$,且$x_{1}x_{2}x_{3}=-1$.其中,所有正确结论的序号是______.
答案:
14.②③ [解析] 本题考查函数性质的综合运用
思路探寻
由题意结合函数单调性的概念举出反例可判断①
$x_1=\frac{b - 1}{a}$,$x_2=e^{-b}$,$x_3=e^b$
令$x_1=\frac{b - 1}{a}=-1$,验证后,即可判断③,即可得解.
对于①,当$a=-2$时,因为$0<e^{-2}<1$,$f(0)=1<f(e^{-2})=\vert\ln e^{-2}\vert=2$,所以函数$f(x)$在区间$(-\infty,1)$上不单调递减,故①错误;
对于②,函数$f(x)=\begin{cases}ax + 1,x\leq0,\\\vert\ln x\vert,x>0,\end{cases}$可转化为$f(x)=\begin{cases}ax + 1,x\leq0,\\-\ln x,0<x\leq1,\\\ln x,x>1,\end{cases}$
画出函数$f(x)$的图象,如图所示,
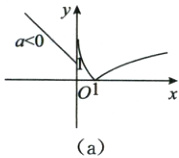
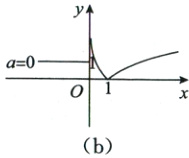
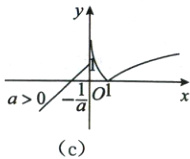
由图象得,若函数$f(x)$无最小值,则$a$的取值范围为$(0,+\infty)$,故②正确;
对于③,令$y=f(x)-b=0$,得$f(x)=b$,结合函数$f(x)$的图象,不妨设$x_1<0<x_2<1<x_3$,则$ax_1 + 1=-\ln x_2=\ln x_3=b$,所以$x_1=\frac{b - 1}{a}$,$x_2=e^{-b}$,$x_3=e^b$,
所以$x_2· x_3=e^{-b}· e^b=1$,所以$x_1=\frac{b - 1}{a}=-1$,得$b=-a + 1$,
当$a<0$时,$b=-a + 1>1$,$y=f(x)-b=0$存在3个零点,且$x_1x_2x_3=-1$,符合题意,
当$0<a<1$时,$0<b=-a + 1<1$,$y=f(x)-b=0$存在3个零点,且$x_1x_2x_3=-1$,符合题意,故③正确.故答案为②③.
14.②③ [解析] 本题考查函数性质的综合运用
思路探寻
由题意结合函数单调性的概念举出反例可判断①
$x_1=\frac{b - 1}{a}$,$x_2=e^{-b}$,$x_3=e^b$
令$x_1=\frac{b - 1}{a}=-1$,验证后,即可判断③,即可得解.
对于①,当$a=-2$时,因为$0<e^{-2}<1$,$f(0)=1<f(e^{-2})=\vert\ln e^{-2}\vert=2$,所以函数$f(x)$在区间$(-\infty,1)$上不单调递减,故①错误;
对于②,函数$f(x)=\begin{cases}ax + 1,x\leq0,\\\vert\ln x\vert,x>0,\end{cases}$可转化为$f(x)=\begin{cases}ax + 1,x\leq0,\\-\ln x,0<x\leq1,\\\ln x,x>1,\end{cases}$
画出函数$f(x)$的图象,如图所示,



由图象得,若函数$f(x)$无最小值,则$a$的取值范围为$(0,+\infty)$,故②正确;
对于③,令$y=f(x)-b=0$,得$f(x)=b$,结合函数$f(x)$的图象,不妨设$x_1<0<x_2<1<x_3$,则$ax_1 + 1=-\ln x_2=\ln x_3=b$,所以$x_1=\frac{b - 1}{a}$,$x_2=e^{-b}$,$x_3=e^b$,
所以$x_2· x_3=e^{-b}· e^b=1$,所以$x_1=\frac{b - 1}{a}=-1$,得$b=-a + 1$,
当$a<0$时,$b=-a + 1>1$,$y=f(x)-b=0$存在3个零点,且$x_1x_2x_3=-1$,符合题意,
当$0<a<1$时,$0<b=-a + 1<1$,$y=f(x)-b=0$存在3个零点,且$x_1x_2x_3=-1$,符合题意,故③正确.故答案为②③.
查看更多完整答案,请扫码查看


