2025年期中期末名校名区真题精编高一数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年期中期末名校名区真题精编高一数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 如图是某市夏季某一天的温度变化曲线(部分),若该曲线近似为函数 $ y = A\sin(\omega x + \varphi) + B(0 < \varphi < \pi) $ 的图象的一部分,则下列说法正确的是(
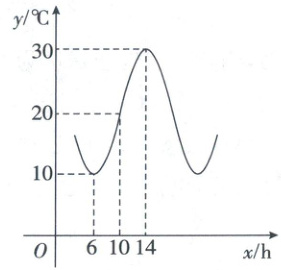
A.该函数的周期是 16
B.该函数图象的一条对称轴是直线 $ x = 14 $
C.温度变化曲线对应的函数解析式是 $ y = 10\sin(\frac{\pi}{8}x + \frac{3\pi}{4}) + 20(0 \leq x \leq 24) $
D.这一天的函数关系式也适用于第二天
ABC
)
A.该函数的周期是 16
B.该函数图象的一条对称轴是直线 $ x = 14 $
C.温度变化曲线对应的函数解析式是 $ y = 10\sin(\frac{\pi}{8}x + \frac{3\pi}{4}) + 20(0 \leq x \leq 24) $
D.这一天的函数关系式也适用于第二天
答案:
10.ABC本题考查正弦型函数的性质 由题意以及函数的图象可知,A + B = 30,−A + B = 10,解得A = 10,B = 20.因为$\frac{T}{2}$ = 14 - 6(T为函数的最小正周期),所以T = 16,所以A正确.易知B正确.因为T = $\frac{2\pi}{|\omega|}$,所以ω = ± $\frac{\pi}{8}$.当ω = $\frac{\pi}{8}$时,y = 10 sin($\frac{\pi}{8}$x + φ) + 20,因为图象经过点(14, 30),所以30 = 10 sin($\frac{\pi}{8}$ × 14 + φ) + 20,所以sin($\frac{\pi}{8}$ × 14 + φ) = 1,所以φ = −$\frac{5}{4}$π + 2kπ,k∈Z.因为0 < φ < π,所以φ = $\frac{3\pi}{4}$,所以y = 10 sin($\frac{\pi}{8}$x + $\frac{3\pi}{4}$) + 20;当ω = −$\frac{\pi}{8}$时,y = 10 sin(−$\frac{\pi}{8}$x + φ) + 20,把(14, 30)代入得sin(−$\frac{\pi}{8}$ × 14 + φ) = 1,所以φ = $\frac{9\pi}{4}$ + 2kπ,k∈Z.因为0 < φ < π,所以φ = $\frac{\pi}{4}$,所以y = 10 sin(−$\frac{\pi}{8}$x + $\frac{\pi}{4}$) + 20 = -10 sin($\frac{\pi}{8}$x - $\frac{\pi}{4}$) + 20 = 10 sin($\frac{\pi}{8}$x - $\frac{\pi}{4}$ + π) + 20 = 10 sin($\frac{\pi}{8}$x + $\frac{3\pi}{4}$) + 20.综上可得,温度变化曲线对应的函数解析式为y = 10 sin($\frac{\pi}{8}$x + $\frac{3\pi}{4}$) + 20 (0 ≤ x ≤ 24),所以C正确.这一天的函数关系式只适用于当天,第二天这个函数关系式不一定适用,故D不正确.故选ABC.
11. 已知函数 $ f(x) = \begin{cases} \log_{2}x, x > 0, \\ 3^{x}, x \leq 0, \end{cases} $ 关于 $ x $ 的方程 $ f(x) + x - a = 0 $ 有且只有一个实根,则实数 $ a $ 的取值是( )
A.$ -1 $
B.0
C.2
D.3
A.$ -1 $
B.0
C.2
D.3
答案:
11.CD本题考查将方程的根转化为函数图象的交点求参数的取值范围问题 方程f(x)+x−a=0有且只有一个实根,等价于函数y=f(x)的图象与直线y=−x + a有且只有一个交点,作出两函数的图象,如图,结合函数图象可知,当a≤1时,两函数图象有两个交点,当a>1时,两函数图象有且只有一个交点.故选CD.

11.CD本题考查将方程的根转化为函数图象的交点求参数的取值范围问题 方程f(x)+x−a=0有且只有一个实根,等价于函数y=f(x)的图象与直线y=−x + a有且只有一个交点,作出两函数的图象,如图,结合函数图象可知,当a≤1时,两函数图象有两个交点,当a>1时,两函数图象有且只有一个交点.故选CD.

12. 将函数 $ y = \sin(2x + \frac{\pi}{4}) $ 的图象上各点的横坐标伸长到原来的 2 倍(纵坐标不变),再向右平移 $ \frac{\pi}{4} $ 个单位长度,所得到的图象对应的函数解析式是
y=sinx
.
答案:
12.y=sinx [解析] 本题考查三角函数图象变换 函数y=sin(2x+$\frac{π}{4}$)的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,得到y=sin(x+$\frac{π}{4}$)的图象,再向右平移$\frac{π}{4}$个单位长度,得到y=sin(x−$\frac{π}{4}$+$\frac{π}{4}$)=sinx的图象,故最终所得到的图象对应的函数解析式为y=sinx.
13. 奇函数 $ f(x) $ 是定义在 $ [-2, 2] $ 上的减函数,若 $ f(2a + 1) + f(4a - 3) > 0 $,则实数 $ a $ 的取值范围是
[$\frac{1}{4}$,$\frac{1}{3}$)
.
答案:
13.[$\frac{1}{4}$,$\frac{1}{3}$) [解析] 本题考查抽象函数的单调性和奇偶性 由f(2a + 1) + f(4a - 3) > 0得f(2a + 1) > -f(4a - 3),因为f(x)为奇函数,所以−f(4a - 3)=f(3 - 4a),所以f(2a + 1) > f(3 - 4a),又f(x)是定义在[−2,2]上的减函数,所以$\begin{cases} 2 \geq 3 - 4a, \\ 3 - 4a > 2a + 1, \\ 2a + 1 \geq -2, \end{cases}$解得$\frac{1}{4}$ ≤ a < $\frac{1}{3}$,即a∈[$\frac{1}{4}$,$\frac{1}{3}$).
14. 已知函数 $ f(x) = |\sin x| - \cos x $,给出以下四个命题:
① $ f(x) $ 的图象关于 $ y $ 轴对称;
② $ f(x) $ 在 $ [-\pi, 0] $ 上是减函数;
③ $ f(x) $ 是周期函数;
④ $ f(x) $ 在 $ [-\pi, \pi] $ 上恰有三个零点.
其中真命题的序号是
① $ f(x) $ 的图象关于 $ y $ 轴对称;
② $ f(x) $ 在 $ [-\pi, 0] $ 上是减函数;
③ $ f(x) $ 是周期函数;
④ $ f(x) $ 在 $ [-\pi, \pi] $ 上恰有三个零点.
其中真命题的序号是
①③
.
答案:
14.①③ [解析] 本题考查含绝对值三角函数的性质 对于①,函数f(x)=|sinx|−cosx的定义域为R,且满足f(−x)=f(x),所以f(x)是定义在R上的偶函数,其图象关于y轴对称,①为真命题;对于②,当x∈[−π,0]时,sinx≤0,f(x)=−(sinx+cosx)=−$\sqrt{2}$sin(x+$\frac{π}{4}$),对于y=$\sqrt{2}$sin(x+$\frac{π}{4}$),x+$\frac{π}{4}$∈[−$\frac{3π}{4}$,$\frac{π}{4}$],易知函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)在[−π,0]上先减后增,那么f(x)在[−π,0]上先增后减,②为假命题;对于③,因为f(x+2π)=|sin(x+2π)|−cos(x+2π)=|sinx|−cosx=f(x),所以函数f(x)是周期为2π的周期函数,③为真命题;对于④,当x∈[−π,0]时,sinx≤0,f(x)=−(sinx+cosx)=−$\sqrt{2}$sin(x+$\frac{π}{4}$),且x+$\frac{π}{4}$∈[−$\frac{3π}{4}$,$\frac{π}{4}$],f(x)在[−π,0]上恰有一个零点,为−$\frac{π}{4}$,又由①知f(x)是定义在R上的偶函数,所以f(x)在(0,π]上也恰有一个零点,为$\frac{π}{4}$,则④为假命题.
15. (13 分)已知集合 $ A = \{ x | 2 - a \leq x \leq 2 + a \} $,$ B = \{ x | x^{2} - 5x + 4 \geq 0 \} $.
(1)当 $ a = 3 $ 时,求 $ A \cap B $,$ A \cup (\complement_{\mathbf{R}}B) $;
(2)若 $ A \cap B = \varnothing $,求实数 $ a $ 的取值范围.
(1)当 $ a = 3 $ 时,求 $ A \cap B $,$ A \cup (\complement_{\mathbf{R}}B) $;
(2)若 $ A \cap B = \varnothing $,求实数 $ a $ 的取值范围.
答案:
15.[解析] 本题考查集合的综合运算、一元二次不等式的解法
(1)当a = 3时,A = {x | 2 - a ≤ x ≤ 2 + a} = {x | -1 ≤ x ≤ 5},B = {x | x² - 5x + 4 ≥ 0} = {x | x ≤ 1 或 x ≥ 4},所以A ∩ B = {x | -1 ≤ x ≤ 1 或 4 ≤ x ≤ 5}. 因为∁$_{R}$B = {x | 1 < x < 4},所以A ∪ (∁$_{R}$B) = {x | -1 ≤ x ≤ 5}.
(2)当2 - a > 2 + a,即a < 0时,A = ∅,满足题意;当a ≥ 0时,应满足$\begin{cases} 2 - a > 1, \\ 2 + a < 4, \end{cases}$解得0 ≤ a < 1. 综上,实数a的取值范围是(−∞,1).
(1)当a = 3时,A = {x | 2 - a ≤ x ≤ 2 + a} = {x | -1 ≤ x ≤ 5},B = {x | x² - 5x + 4 ≥ 0} = {x | x ≤ 1 或 x ≥ 4},所以A ∩ B = {x | -1 ≤ x ≤ 1 或 4 ≤ x ≤ 5}. 因为∁$_{R}$B = {x | 1 < x < 4},所以A ∪ (∁$_{R}$B) = {x | -1 ≤ x ≤ 5}.
(2)当2 - a > 2 + a,即a < 0时,A = ∅,满足题意;当a ≥ 0时,应满足$\begin{cases} 2 - a > 1, \\ 2 + a < 4, \end{cases}$解得0 ≤ a < 1. 综上,实数a的取值范围是(−∞,1).
查看更多完整答案,请扫码查看


