《2025年期中期末名校名区真题精编高一数学上册人教版》

15. （13分）已知函数$f(x)=2\sqrt{3}\sin x\cos x+\cos^{2}x-\sin^{2}x + a(x\in R)$的最大值为5.
（1）求$a$的值和$f(x)$的最小正周期；
（2）求$f(x)$的单调递增区间.

答案： 15.[解析] 本题考查三角恒等变换与三角函数的性质的综合
(1)$f(x)=\sqrt{3}\sin2x+\cos2x+a=2\sin(2x+\frac{\pi}{6})+a$，由题意，得$2 + a = 5$，解得$a = 3$，$T=\frac{2\pi}{2}=\pi$.
故$a = 3$，$f(x)$的最小正周期为$\pi$.
(2)令$2k\pi-\frac{\pi}{2}\leq2x+\frac{\pi}{6}\leq2k\pi+\frac{\pi}{2},k\in\mathbf{Z}$，
解得$k\pi-\frac{\pi}{3}\leq x\leq k\pi+\frac{\pi}{6},k\in\mathbf{Z}$，
所以$f(x)$的单调递增区间为$[k\pi-\frac{\pi}{3},k\pi+\frac{\pi}{6}],k\in\mathbf{Z}$.

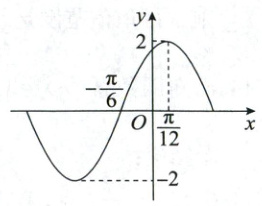
16. （15分）已知函数$f(x)=A\sin(\omega x+\varphi)(A＞0,\omega＞0,\vert\varphi\vert＜\frac{\pi}{2})$的部分图象如图所示.
（1）求函数$f(x)$的解析式；
（2）将函数$y = f(x)$的图象上各点的横坐标缩短到原来的$\frac{1}{2}$，纵坐标不变，得到函数$y = g(x)$的图象，求函数$y = g(x)$在区间$[0,\frac{\pi}{4}]$上的最大值及函数取最大值时相应的$x$的值.

答案： 16.[解析] 本题考查由三角函数图象求解析式、三角函数的最值问题
(1)由题图可知，$A = 2$，$T = 4×[\frac{\pi}{12}-(-\frac{\pi}{6})]=\pi$，
所以$\omega=\frac{2\pi}{T}=2$，所以$f(x)=2\sin(2x+\varphi)$.
又因为$\begin{cases}2\sin(2×\frac{\pi}{12}+\varphi)=2,\\\vert\varphi\vert＜\frac{\pi}{2},\end{cases}$所以$\varphi=\frac{\pi}{3}$，
所以函数$f(x)$的解析式为$f(x)=2\sin(2x+\frac{\pi}{3})$.
(2)依题意，得$g(x)=2\sin(4x+\frac{\pi}{3})$，因为$x\in[0,\frac{\pi}{4}]$，
所以$4x+\frac{\pi}{3}\in[\frac{\pi}{3},\frac{4\pi}{3}]$，易知当$4x+\frac{\pi}{3}=\frac{\pi}{2}$，即$x=\frac{\pi}{24}$时，函数$g(x)$在$[0,\frac{\pi}{4}]$上取得最大值，最大值为$g(\frac{\pi}{24})=2$.

17. （15分）已知函数$g(x)=ax^{2}-2ax + 1 + b(a＞0)$在区间$[2,3]$上有最大值4和最小值1，设$f(x)=\frac{g(x)}{x}$.
（1）求$a,b$的值；
（2）若不等式$f(2^{x})-k·2^{x}\geq0$在$x\in[-1,1]$上有解，求实数$k$的取值范围.

答案： 17.[解析] 本题考查二次函数的最值、不等式能成立问题
(1)$g(x)=a(x - 1)^2+1 + b - a$，其图象的对称轴为直线$x = 1$，
因为$a＞0$，所以$g(x)$在$[2,3]$上单调递增，
所以$\begin{cases}g(2)=1 + b = 1,\\g(3)=3a + 1 + b = 4,\end{cases}$解得$\begin{cases}a = 1,\\b = 0.\end{cases}$
(2)由
(1)知$g(x)=x^2-2x + 1$，
则$f(x)=x+\frac{1}{x}-2(x\neq0)$，
所以$f(2^x)-k·2^x\geq0$即为$2^x+\frac{1}{2^x}-2\geq k·2^x$，
即$1+(\frac{1}{2^x})^2-2·\frac{1}{2^x}\geq k$，
令$t=\frac{1}{2^x},t\in[\frac{1}{2},2]$（因为$x\in[-1,1]$，所以$2^x\in[\frac{1}{2},2]$，则$t=\frac{1}{2^x}\in[\frac{1}{2},2]$），则$k\leq t^2-2t + 1$，
故问题可转化为$k\leq(t^2-2t + 1)_{\max},t\in[\frac{1}{2},2]$，
令$h(t)=t^2-2t + 1,t\in[\frac{1}{2},2]$，其图象的对称轴是直线$t = 1$，所以$h(t)_{\max}=h(2)=1$，所以$k\leq1$.
故实数$k$的取值范围为$(-\infty,1]$.
名师点拨
本题第
(2)问是不等式有解问题，一般情况下，可通过分离变量转化为求函数的最值问题，从而得参数的取值范围.