《2025年课堂精练七年级数学上册北师大版》

1. 规定了______、______和______的直线称为数轴。通常将数轴画成______,并选择______的方向为正方向。
2. 任何一个有理数都可以用数轴上的一个______来表示。
3. 数轴上两个点表示的数,______总比______大。
4. 一个数的绝对值就是这个数所对应的______。

答案： 1. 原点 单位长度 正方向 水平直线 向右 2. 点 3. 右边的 左边的 4. 点到原点的距离

1. 下列图形是数轴的是( )。
]

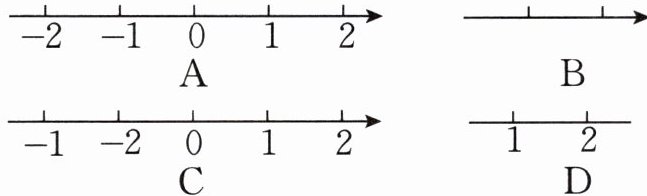
答案： A

2. 如图,点M表示的数可能是( )。


A.1.5
B.-1.5
C.2.5
D.-2.5

答案： D

3. 若a＞b＞0,则在数轴上表示数a,b正确的是( )。
]

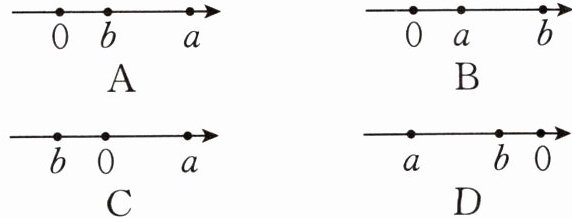
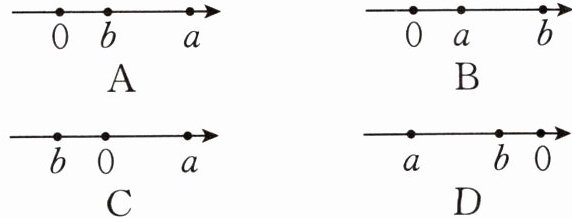
答案： A

4. 下列说法正确的是( )。

A.数轴上的一个点可以表示两个不同的有理数
B.数轴上有两个不同的点表示同一个有理数
C.任何一个有理数都可以用数轴上的一个点来表示
D.有的有理数不能在数轴上表示出来

答案： C

5. 在数轴上,原点及原点右边的点表示的数是( )。

A.正数
B.负数
C.正整数
D.非负数

答案： D

6. a,b在数轴上的对应点的位置如图所示,则下面结论正确的是( )。


A.a＞-2
B.a＜-3
C.a＞-b
D.a＜-b

答案： D

7. 在数轴上表示下列各数,并用“＜”将它们连接起来：-3,-1.5,$\frac{1}{2}$,0,-2$\frac{1}{2}$,2.5。

答案： 解:数轴略,$-3＜-2\dfrac{1}{2}＜-1.5＜0＜\dfrac{1}{2}＜2.5$。

8. 如图,四个有理数在数轴上的对应点分别为M,P,N,Q。若点M,N表示的有理数互为相反数,则图中的点表示的数中,绝对值最小的是( )。


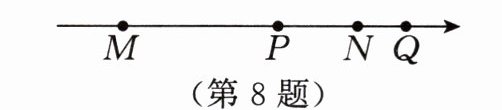
A.点M
B.点N
C.点P
D.点Q

答案： C