第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
6. 合理分类和利用垃圾可以保护环境、变废为宝。在一定条件下, $ 1 \, t $ 分类后的垃圾能“榨”出 $ 140 \, kg $ 的燃料油,若该燃料油完全燃烧能释放 $ 5.6×10^{9} \, J $ 的热量。(对应目标:911304)
(1)求 $ 1 \, t $ 垃圾“榨”出的燃料油的热值。
(2)在一个标准大气压下,这些热量的 $ 30\% $ 被质量为 $ 5×10^{3} \, kg $、初温为 $ 30 \, ℃ $ 的水吸收,则吸收热量后水的温度为多少? $ [c_{水} = 4.2×10^{3} \, J/(kg·℃)] $
(1)求 $ 1 \, t $ 垃圾“榨”出的燃料油的热值。
(2)在一个标准大气压下,这些热量的 $ 30\% $ 被质量为 $ 5×10^{3} \, kg $、初温为 $ 30 \, ℃ $ 的水吸收,则吸收热量后水的温度为多少? $ [c_{水} = 4.2×10^{3} \, J/(kg·℃)] $
答案:
解:(1)垃圾“榨”出的燃料油的热值q=Q放/m=5.6×10⁹J/140kg=4.0×10⁷J/kg。(2)水吸收的热量Q吸=ηQ放=30%×5.6×10⁹J=1.68×10⁹J,由Q=cmΔt得,水升高的温度Δt=Q吸/c水m水=1.68×10⁹J/(4.2×10³J/(kg·℃)×5×10³kg)=80℃,水的温度t=30℃+80℃=110℃,在一个标准大气压下,水的沸点为100℃,故水温升高到100℃,即吸收热量后水的温度是100℃。
7. 给质量为 $ m_{A} $、比热容为 $ c_{A} $ 的物体 $ A $ 和质量为 $ m_{B} $、比热容为 $ c_{B} $ 的物体 $ B $ 加热,加热源和加热方式都相同,物体 $ A $、$ B $ 的温度随加热时间的变化如图 1 - 3 - 5 所示,根据图像可得出的正确结论是(
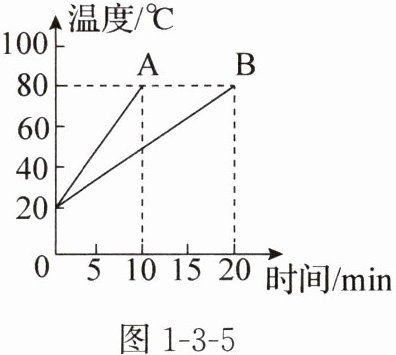
A.若 $ c_{A} = c_{B} $,则 $ m_{A} > m_{B} $
B.若 $ c_{A} = c_{B} $,则 $ m_{A} < m_{B} $
C.若 $ m_{A} = m_{B} $,则 $ c_{A} > c_{B} $
D.若 $ m_{A} > m_{B} $,则 $ c_{A} > c_{B} $
B
)。(对应目标:911304)
A.若 $ c_{A} = c_{B} $,则 $ m_{A} > m_{B} $
B.若 $ c_{A} = c_{B} $,则 $ m_{A} < m_{B} $
C.若 $ m_{A} = m_{B} $,则 $ c_{A} > c_{B} $
D.若 $ m_{A} > m_{B} $,则 $ c_{A} > c_{B} $
答案:
B
8. $ A $、$ B $ 两物体的质量相等,温度均为 $ 10 \, ℃ $;甲、乙两杯水的质量相等,温度均为 $ 50 \, ℃ $。现将 $ A $ 放入甲杯,$ B $ 放入乙杯,热平衡后,甲杯水温降低了 $ 4 \, ℃ $,乙杯水温降低了 $ 10 \, ℃ $,不考虑热量的损耗,则 $ A $、$ B $ 两物体的比热容之比为
1:3
。(对应目标:911304)
答案:
1:3
9. 质量相等的甲、乙两金属球,用酒精灯加热至相同温度后,先将甲球投入一杯冷水中,待热平衡后水温升高 $ \Delta t_{1} \, ℃ $,此时甲球放出的热量为 $ Q_{甲} $;然后迅速把乙球投入水中(甲球未取出),热平衡后水温又升高 $ \Delta t_{2} \, ℃ $,此时乙球放出的热量为 $ Q_{乙} $。若 $ Q_{甲} = Q_{乙} $ 且不计热量损失及水的质量损失,则 $ \Delta t_{1} $
>
$ \Delta t_{2} $,甲、乙两球的比热容 $ c_{甲} $<
$ c_{乙} $。(两空均选填“$ > $”“$ < $”或“$ = $”)(对应目标:911304)
答案:
> <
10. 冬天即将来临,学校积极创造条件为学生供应热水。在这个过程中,若用电子温控锅炉将 $ 300 \, kg $ 的水从 $ 20 \, ℃ $ 加热到 $ 70 \, ℃ $,燃烧了 $ 8.4 \, kg $ 的煤,已知 $ c_{水} = 4.2×10^{3} \, J/(kg·℃) $,煤的热值为 $ 3×10^{7} \, J/kg $。(对应目标:911304)
(1)求锅炉内的水吸收的热量。
(2)某同学打了 $ 4 \, kg $ 的 $ 70 \, ℃ $ 的热水,为了便于使用,他将这些热水和质量为 $ 6 \, kg $ 的 $ 20 \, ℃ $ 的冷水混合,若不计混合过程的热损失,则混合后温水的温度为多少?
(1)求锅炉内的水吸收的热量。
(2)某同学打了 $ 4 \, kg $ 的 $ 70 \, ℃ $ 的热水,为了便于使用,他将这些热水和质量为 $ 6 \, kg $ 的 $ 20 \, ℃ $ 的冷水混合,若不计混合过程的热损失,则混合后温水的温度为多少?
答案:
解:(1)锅炉内的水吸收的热量Q吸=c水m(t-t₀)=4.2×10³J/(kg·℃)×300kg×(70℃-20℃)=6.3×10⁷J。(2)设冷水温度从20℃升高到t,吸收的热量为Q₁;热水温度从70℃降低到t,放出的热量为Q₂,由于不计热损失,则Q₁=Q₂,即c水m₁(t-20℃)=c水m₂(70℃-t),4.2×10³J/(kg·℃)×6kg×(t-20℃)=4.2×10³J/(kg·℃)×4kg×(70℃-t),解得t=40℃。
查看更多完整答案,请扫码查看


