第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
4. 已知$x+\dfrac{1}{x}= 2+\sqrt{10}$. 求$x^2+\dfrac{1}{x^2}$的值.
答案:
$12+4\sqrt{10}$
5. 教师节到了,为表达对老师的感谢,小刚做了两张大小不同的正方形贺卡,其中一张的面积为$800\ cm^2$,另一张的面积为$450\ cm^2$. 他想,如果再用金彩带把贺卡的边缘镶上会更漂亮. 现在他只有一根$1.2\ m$长的金彩带,请你帮他算一算这根金彩带是否够用. 如果不够用,还需要多少厘米长的金彩带?$(\sqrt{2}\approx1.414$,结果保留整数$)$
答案:
这根金彩带不够用,还需要约78 cm长的金彩带.
6. 先观察下面的化简过程,感受分母有理化的作用,再回答问题.
$\dfrac{1}{\sqrt{5}+\sqrt{4}}= \dfrac{1×(\sqrt{5}-\sqrt{4})}{(\sqrt{5}+\sqrt{4})(\sqrt{5}-\sqrt{4})}= \sqrt{5}-\sqrt{4}= \sqrt{5}-2$,
$\dfrac{1}{\sqrt{6}+\sqrt{5}}= \dfrac{1×(\sqrt{6}-\sqrt{5})}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}= \sqrt{6}-\sqrt{5}$.
(1)请写出化简$\dfrac{1}{\sqrt{n}+\sqrt{n - 1}}$的结果.
(2)化简:$\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+…+\dfrac{1}{\sqrt{98}+\sqrt{99}}+\dfrac{1}{\sqrt{99}+\sqrt{100}}$.
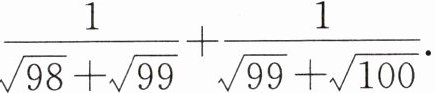
(3)不计算近似值,试比较$\sqrt{13}-\sqrt{11}与\sqrt{15}-\sqrt{13}$的大小,并说明理由.
$\dfrac{1}{\sqrt{5}+\sqrt{4}}= \dfrac{1×(\sqrt{5}-\sqrt{4})}{(\sqrt{5}+\sqrt{4})(\sqrt{5}-\sqrt{4})}= \sqrt{5}-\sqrt{4}= \sqrt{5}-2$,
$\dfrac{1}{\sqrt{6}+\sqrt{5}}= \dfrac{1×(\sqrt{6}-\sqrt{5})}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}= \sqrt{6}-\sqrt{5}$.
(1)请写出化简$\dfrac{1}{\sqrt{n}+\sqrt{n - 1}}$的结果.
(2)化简:$\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+…+\dfrac{1}{\sqrt{98}+\sqrt{99}}+\dfrac{1}{\sqrt{99}+\sqrt{100}}$.
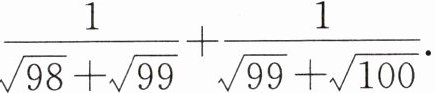
(3)不计算近似值,试比较$\sqrt{13}-\sqrt{11}与\sqrt{15}-\sqrt{13}$的大小,并说明理由.
答案:
(1)$\sqrt{n}-\sqrt{n-1}$
(2)9
(3)$\sqrt{13}-\sqrt{11}>\sqrt{15}-\sqrt{13}$,理由略.
(1)$\sqrt{n}-\sqrt{n-1}$
(2)9
(3)$\sqrt{13}-\sqrt{11}>\sqrt{15}-\sqrt{13}$,理由略.
查看更多完整答案,请扫码查看


