第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
6. 已知:如图,四边形$ABCD$为正方形,从顶点$A引两条射线分别交BC$,$CD于点E$,$F$,$\angle EAF = 45^{\circ}$.
求证:$BE + DF = EF$.

求证:$BE + DF = EF$.

答案:
证明:如图,延长CD到点G,使$DG=BE$,连接AG.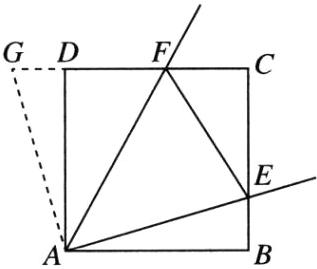
∵四边形ABCD为正方形,$\therefore AB=AD,∠B=∠ADC=∠BAD=90^{\circ }.$ $\therefore ∠ADG=90^{\circ }=∠B.$ 在$\triangle ABE$和$\triangle ADG$中, $\left\{\begin{array}{l} AB=AD,\\ ∠B=∠ADG,\\ BE=DG,\end{array}\right. $ $\therefore \triangle ABE\cong \triangle ADG(SAS).$ $\therefore AE=AG,∠BAE=∠DAG.$ $\because ∠EAF=45^{\circ },$ $\therefore ∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90^{\circ }-45^{\circ }=45^{\circ }.$ $\therefore ∠EAF=∠GAF.$ 在$\triangle AEF$和$\triangle AGF$中, $\left\{\begin{array}{l} AE=AG,\\ ∠EAF=∠GAF,\\ AF=AF,\end{array}\right. $ $\therefore \triangle AEF\cong \triangle AGF(SAS).$ $\therefore EF=GF.$ $\because GF=DG+DF=BE+DF,$ $\therefore BE+DF=EF.$
证明:如图,延长CD到点G,使$DG=BE$,连接AG.

∵四边形ABCD为正方形,$\therefore AB=AD,∠B=∠ADC=∠BAD=90^{\circ }.$ $\therefore ∠ADG=90^{\circ }=∠B.$ 在$\triangle ABE$和$\triangle ADG$中, $\left\{\begin{array}{l} AB=AD,\\ ∠B=∠ADG,\\ BE=DG,\end{array}\right. $ $\therefore \triangle ABE\cong \triangle ADG(SAS).$ $\therefore AE=AG,∠BAE=∠DAG.$ $\because ∠EAF=45^{\circ },$ $\therefore ∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90^{\circ }-45^{\circ }=45^{\circ }.$ $\therefore ∠EAF=∠GAF.$ 在$\triangle AEF$和$\triangle AGF$中, $\left\{\begin{array}{l} AE=AG,\\ ∠EAF=∠GAF,\\ AF=AF,\end{array}\right. $ $\therefore \triangle AEF\cong \triangle AGF(SAS).$ $\therefore EF=GF.$ $\because GF=DG+DF=BE+DF,$ $\therefore BE+DF=EF.$
7. 在$\triangle ABC$中,$AC = BC$,$\angle ACB = 90^{\circ}$,$D是AB$的中点,$E是AB$上一点.
(1)如图①,若$BF\perp CE于点F$,$BF交CD于点G$,求证:$AE = CG$.
(2)如图②,若$AM\perp CE$,$AM交CE的延长线于点H$,交$CD的延长线于点M$,请找出图中与$BE$相等的线段,并证明.

(1)如图①,若$BF\perp CE于点F$,$BF交CD于点G$,求证:$AE = CG$.
(2)如图②,若$AM\perp CE$,$AM交CE的延长线于点H$,交$CD的延长线于点M$,请找出图中与$BE$相等的线段,并证明.

答案:
(1)证明:
∵D是AB的中点,$\therefore AD=BD.$ 又$\because AC=BC,CD=CD,$ $\therefore \triangle ACD\cong \triangle BCD(SSS).$ $\therefore ∠ACD=∠BCD=45^{\circ },∠CAD=∠CBD=45^{\circ }.$ $\therefore ∠CAE=∠BCG.$ $\because BF⊥CE,$ $\therefore ∠BFC=90^{\circ }.$ $\therefore ∠CBG+∠BCF=90^{\circ }.$ 又$\because ∠ACE+∠BCF=90^{\circ },$ $\therefore ∠ACE=∠CBG.$ 又$\because AC=BC,$ $\therefore \triangle AEC\cong \triangle CGB(ASA).$ $\therefore AE=CG.$
(2)$CM=BE.$ 证明:由
(1),知$∠ADC=90^{\circ },$ $\therefore ∠BEC+∠MCH=90^{\circ }.$ $\because CH⊥HM,$ $\therefore ∠CHM=90^{\circ }.$ $\therefore ∠CMA+∠MCH=90^{\circ }.$ $\therefore ∠CMA=∠BEC.$ 由
(1),知$∠ACM=∠CBE=45^{\circ }.$ 在$\triangle CAM$和$\triangle BCE$中, $\left\{\begin{array}{l} ∠CMA=∠BEC,\\ ∠ACM=∠CBE,\\ CA=BC,\end{array}\right. $ $\therefore \triangle CAM\cong \triangle BCE(AAS).$ $\therefore CM=BE.$
(1)证明:
∵D是AB的中点,$\therefore AD=BD.$ 又$\because AC=BC,CD=CD,$ $\therefore \triangle ACD\cong \triangle BCD(SSS).$ $\therefore ∠ACD=∠BCD=45^{\circ },∠CAD=∠CBD=45^{\circ }.$ $\therefore ∠CAE=∠BCG.$ $\because BF⊥CE,$ $\therefore ∠BFC=90^{\circ }.$ $\therefore ∠CBG+∠BCF=90^{\circ }.$ 又$\because ∠ACE+∠BCF=90^{\circ },$ $\therefore ∠ACE=∠CBG.$ 又$\because AC=BC,$ $\therefore \triangle AEC\cong \triangle CGB(ASA).$ $\therefore AE=CG.$
(2)$CM=BE.$ 证明:由
(1),知$∠ADC=90^{\circ },$ $\therefore ∠BEC+∠MCH=90^{\circ }.$ $\because CH⊥HM,$ $\therefore ∠CHM=90^{\circ }.$ $\therefore ∠CMA+∠MCH=90^{\circ }.$ $\therefore ∠CMA=∠BEC.$ 由
(1),知$∠ACM=∠CBE=45^{\circ }.$ 在$\triangle CAM$和$\triangle BCE$中, $\left\{\begin{array}{l} ∠CMA=∠BEC,\\ ∠ACM=∠CBE,\\ CA=BC,\end{array}\right. $ $\therefore \triangle CAM\cong \triangle BCE(AAS).$ $\therefore CM=BE.$
8. 如图,$\triangle ABC的两条高AD与BE相交于点O$,$AD = BD$,$AC = 6$.
(1)求$BO$的长.
(2)$F是射线BC$上一点,且$CF = AO$,动点$P从点O$出发,沿线段$OB以每秒1个单位长度的速度向终点B$运动,同时动点$Q从点A$出发,沿射线$AC以每秒4$个单位长度的速度运动(点$F$,$P$,$Q$没画出). 当点$P到达点B$时,$P$,$Q$两点同时停止运动. 设运动时间为$t\ s$,当$\triangle AOP\cong \triangle FCQ$时,求$t$的值.

(1)求$BO$的长.
(2)$F是射线BC$上一点,且$CF = AO$,动点$P从点O$出发,沿线段$OB以每秒1个单位长度的速度向终点B$运动,同时动点$Q从点A$出发,沿射线$AC以每秒4$个单位长度的速度运动(点$F$,$P$,$Q$没画出). 当点$P到达点B$时,$P$,$Q$两点同时停止运动. 设运动时间为$t\ s$,当$\triangle AOP\cong \triangle FCQ$时,求$t$的值.

答案:
解:
(1)$\because ∠CAD+∠ACD=∠CAD+∠AOE=90^{\circ },$ $\therefore ∠ACD=∠AOE.$ $\because ∠AOE=∠BOD,$ $\therefore ∠BOD=∠ACD.$ 又$\because ∠BDO=∠ADC=90^{\circ },AD=BD,$ $\therefore \triangle BDO\cong \triangle ADC(AAS).$ $\therefore BO=AC=6.$
(2)当点F在BC的延长线上时,如图所示. $\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$
$\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$
∴当$\triangle AOP\cong \triangle FCQ$时,$OP=CQ.$ $\because OP=t,CQ=6-4t,$ $\therefore t=6-4t.$ 解得$t=1.2.$ 当点F在BC之间时,如图所示. $\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$
$\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$
∴当$\triangle AOP\cong \triangle FCQ$时,$OP=CQ.$ $\because OP=t,CQ=4t-6,$ $\therefore t=4t-6.$ 解得$t=2.$ 综上所述,$t=1.2$或2.
解:
(1)$\because ∠CAD+∠ACD=∠CAD+∠AOE=90^{\circ },$ $\therefore ∠ACD=∠AOE.$ $\because ∠AOE=∠BOD,$ $\therefore ∠BOD=∠ACD.$ 又$\because ∠BDO=∠ADC=90^{\circ },AD=BD,$ $\therefore \triangle BDO\cong \triangle ADC(AAS).$ $\therefore BO=AC=6.$
(2)当点F在BC的延长线上时,如图所示.
 $\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$
$\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$∴当$\triangle AOP\cong \triangle FCQ$时,$OP=CQ.$ $\because OP=t,CQ=6-4t,$ $\therefore t=6-4t.$ 解得$t=1.2.$ 当点F在BC之间时,如图所示.
 $\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$
$\because CF=AO,∠AOP=∠EOD=180^{\circ }-∠DCE=∠FCQ,$∴当$\triangle AOP\cong \triangle FCQ$时,$OP=CQ.$ $\because OP=t,CQ=4t-6,$ $\therefore t=4t-6.$ 解得$t=2.$ 综上所述,$t=1.2$或2.
查看更多完整答案,请扫码查看


