《2025年同步练习册河北教育出版社八年级数学上册冀教版》

4. 观察下列等式：$\frac{1}{2} = \frac{1}{3} + \frac{1}{6}$,$\frac{1}{3} = \frac{1}{4} + \frac{1}{12}$,$\frac{1}{4} = \frac{1}{5} + \frac{1}{20}$,…$$.
(1)请按照上面的规律归纳出一个一般的结论.(用含$n$的等式表示,$n$是正整数)
(2)请运用分式的有关知识,推理说明这个结论是正确的.

答案：
(1)$\frac{1}{n}=\frac{1}{n+1}+\frac{1}{n(n+1)}$
(2)略

5. 在处理分式的问题时,可以将分式拆分成一个整式与一个分式的和或差的形式,继而解决问题. 我们称这种方法为分离常数法.
示例：将分式$\frac{3x - 2}{x - 1}$分离常数.
解：$\frac{3x - 2}{x - 1} = \frac{3(x - 1) + m}{x - 1} = 3 + \frac{m}{x - 1}$.
(1)在示例中,$m = $1.
(2)参考示例,将分式$\frac{3x + 8}{x + 2}$分离常数.
原式$=\frac{3(x+2)+2}{x+2}=3+\frac{2}{x+2}$.
(3)若$x$为整数,代数式$\frac{x - 2}{x^{2} - 4x + 4} ÷ \frac{1}{x + 6}的值为F$,则$F$的值为整数时,$x$的取值有几个?
$\frac{x-2}{x^{2}-4x+4}÷\frac{1}{x+6}=\frac{x-2}{(x-2)^{2}}·(x+6)=\frac{x+6}{x-2}=1+\frac{8}{x-2}$.
∵代数式$\frac{x-2}{x^{2}-4x+4}÷\frac{1}{x+6}$的值为F，
∴$F=1+\frac{8}{x-2}(x≠2，-6)$.当$x-2=±1，±2，±4，±8$时，即x=3，1，4，0，6，-2，10，-6时，$1+\frac{8}{x-2}$的值为整数. 又$x≠2，-6$，故当x=3，1，4，0，6，-2，10时，F的值为整数，共有7个.

答案：
(1)1
(2)原式$=\frac{3(x+2)+2}{x+2}=3+\frac{2}{x+2}$.
(3)$\frac{x-2}{x^{2}-4x+4}÷\frac{1}{x+6}=\frac{x-2}{(x-2)^{2}}\cdot(x+6)=\frac{x+6}{x-2}=1+\frac{8}{x-2}$.
∵代数式$\frac{x-2}{x^{2}-4x+4}÷\frac{1}{x+6}$的值为F，
∴$F=1+\frac{8}{x-2}(x≠2，-6)$.当$x-2=±1，±2，±4，±8$时，即x=3，1，4，0，6，-2，10，-6时，$1+\frac{8}{x-2}$的值为整数. 又$x≠2，-6$，故当x=3，1，4，0，6，-2，10时，F的值为整数，共有7个.

巧用拆项法

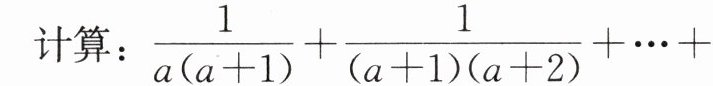
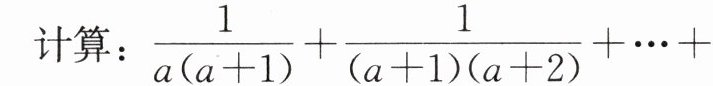
计算：$\frac{1}{a(a + 1)} + \frac{1}{(a + 1)(a + 2)} + … + \frac{1}{(a + 9)(a + 10)}$.
分析：本题中有 10 个分式相加,无法通分,而式子中每个分式的分母都可看作两个连续整数的积(设$a$是整数),由此联想到$\frac{1}{a(a + 1)} = \frac{1}{a} - \frac{1}{a + 1}$,这样可抵消一些项.
解：原式$= \frac{1}{a} - \frac{1}{a + 1} + \frac{1}{a + 1} - \frac{1}{a + 2} + … + \frac{1}{a + 9} - \frac{1}{a + 10}$
$= \frac{1}{a} - \frac{1}{a + 10}$
$= \frac{a + 10 - a}{a(a + 10)}$
$= \frac{10}{a(a + 10)}$.

答案： 解：原式$=\frac{1}{a}-\frac{1}{a+1}+\frac{1}{a+1}-\frac{1}{a+2}+\dots +\frac{1}{a+9}-\frac{1}{a+10}$
$=\frac{1}{a}-\frac{1}{a+10}$
$=\frac{(a+10)-a}{a(a+10)}$
$=\frac{10}{a(a+10)}$