《2025年同步练习册河北教育出版社八年级数学上册冀教版》

4. 判断下列说法是否正确. 若正确,请说明理由；若不正确,请举例说明.
(1)已知两个实数 $a$,$b$,则 $a - b ＜ a$.
(2)两个无理数的积一定是无理数.

答案： 解：
(1)不正确. 反例：$a=3$，$b=-5$，$a-b=8＞3=a$.
(2)不正确. 反例：如果两个无理数互为倒数，那么它们的积为$1$，而$1$是有理数.

5. 若 $a$,$b$ 都是无理数,且 $a + b = 2$,则 $a$,$b$ 的值可以是$1+\sqrt{2}$和$1-\sqrt{2}$(答案不唯一).(写出一组满足条件的值即可)

答案： $1+\sqrt{2}$和$1-\sqrt{2}$(答案不唯一)

6. 将棱长分别为 $10\ cm$ 和 $20\ cm$ 的正方体铁块各三个熔化后再制成一个较大的正方体. 求这个大正方体的棱长.

答案： $30\ cm$

7. 已知一个长方体的体积是 $162$,其长、宽、高的比是 $3:2:1$. 这个长方体的长、宽、高都是无理数吗？请说明理由.

答案： 这个长方体的长、宽、高都不是无理数，说明理由略.

8. 某数值转换器的原理如图所示：

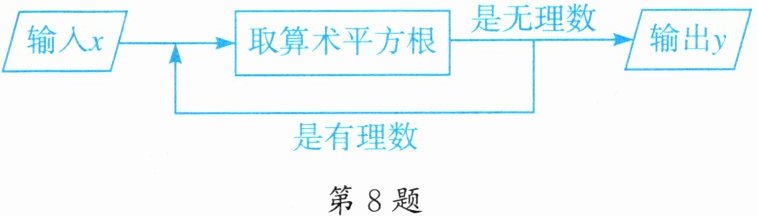
(1)当输入的 $x$ 值为 $16$ 时,求输出的 $y$ 值.
(2)是否存在输入的 $x$ 值,始终不能输出 $y$ 值？如果存在,请直接写出所有满足要求的 $x$ 值；如果不存在,请说明理由.
(3)若输入一个两位数 $x$,恰好经过两次取算术平方根才能输出无理数,则 $x$ 的值可以是多少？(写出一个即可)

答案： 解：
(1)$\sqrt{16}=4$，$\sqrt{4}=2$，则$y=\sqrt{2}$.
(2)$x=0$或$1$时，始终不能输出$y$值.
(3)$x=[(\sqrt{5})^2]^2=25$. (答案不唯一)