《2025年作业本浙江教育出版社五年级数学上册北师大版》

3. 把带分数化成假分数,把假分数化成带分数或整数。
$\frac{35}{9}$ $5\frac{5}{6}$ $\frac{121}{11}$ $8\frac{5}{12}$ $\frac{135}{7}$ $11\frac{1}{10}$

答案： $\frac{35}{9}=3\frac{8}{9}$
$5\frac{5}{6}=\frac{35}{6}$
$\frac{121}{11}=11$
$8\frac{5}{12}=\frac{101}{12}$
$\frac{135}{7}=19\frac{2}{7}$
$11\frac{1}{10}=\frac{111}{10}$

4. 圈出下列分数中的最简分数,并把其余的分数化成最简分数。
$\frac{35}{21}$ $\frac{5}{6}$ $\frac{24}{36}$ $\frac{34}{51}$ $\frac{12}{78}$ $1\frac{16}{45}$

答案： 解析：
最简分数是指分子和分母只有公因数1的分数。
首先，我们圈出最简分数：$\frac{5}{6}$ 和 $1\frac{16}{45}$（因为它们的分子和分母只有公因数1）。
接下来，我们将其余的分数化成最简分数：
1. 对于 $\frac{35}{21}$，分子和分母都可以被7整除，所以化成最简分数为 $\frac{5}{3}$。
2. 对于 $\frac{24}{36}$，分子和分母都可以被12整除，所以化成最简分数为 $\frac{2}{3}$。
3. 对于 $\frac{34}{51}$，分子和分母都可以被17整除，所以化成最简分数为 $\frac{2}{3}$。
4. 对于 $\frac{12}{78}$，分子和分母都可以被6整除，但更精确地说，它们都可以被更大的数（如2, 3, 6的倍数）整除，但最大公因数是6的倍数中的最大者，即2×3=6的某个倍数，这里是2×3×13=78的因数6的倍数中最大的是它们共有的因数最大的是6（但考虑到78是6的13倍，所以直接用78的因数如2、3、6、13、26、39、78来试除，会发现6是合适的最大公因数的一个“代表”，实际我们直接找最大公因数即可，这里是6的“升级版”——考虑78的质因数2、3、13后，知道最大公因数是2×3×(13中分子有的因数1)=6的“扩展”版中最大的那个，即直接通过质因数分解知道最大公因数是2×3×(两者共有的最大质因数群)=2×3=6的“实际应用中我们直接找的那个”26的“前身”——即最大公因数2×3×(13/分子分母共有的质因数中最大的那个对应的“群”)=6(实际是通过质因数分解后，取各自有的质因数中次数最少的那个“群”来相乘，这里就是2、3各一次，13只在分母中有，所以不计入“共有质因数群”)=最终我们知道的用来的那个数——最大公因数6的“代表在实际情况中的最大者”——2×3和13中分子分母都有的那个“部分”的乘积——即6（这里解释过于详细，实际只需知道找最大公因数即可），所以化成最简分数为 $\frac{2}{13}$（因为12和78的最大公因数是6的“实际作用者”——即它们共有的质因数的乘积——这里是2×3=6，所以分子分母都除以6，得到$\frac{2}{13}$）。
答案：
圈出的最简分数有：$\frac{5}{6}$，$1\frac{16}{45}$。
其余分数化成最简分数后为：
$\frac{35}{21} = \frac{5}{3}$；
$\frac{24}{36} = \frac{2}{3}$；
$\frac{34}{51} = \frac{2}{3}$；
$\frac{12}{78} = \frac{2}{13}$。

5. 选择。
(1) 因为60既是12的倍数,又是6的倍数,所以60是12和6的(B)。
A. 公因数 B. 公倍数 C. 最大公因数 D. 最小公倍数
(2) 假分数的分子(C)。
A. 比分母小 B. 比分母大
C. 不小于分母 D. 可以比分母小,也可以比分母大
(3) 下列分数中,与$\frac{5}{7}$不相等的分数是(C)。
A. $\frac{25}{35}$ B. $\frac{35}{49}$ C. $\frac{49}{56}$ D. $\frac{50}{70}$
(4) 分母是8的最简真分数的和是(D)。
A. $3\frac{1}{2}$ B. $4\frac{1}{2}$ C. $\frac{23}{8}$ D. 2

答案： 5.
(1)
解析：根据公倍数的定义，两个或多个整数共有的倍数叫做它们的公倍数。由于60既是12的倍数，又是6的倍数，所以60是12和6的公倍数。
答案：B
(2)
解析：假分数的定义是分子大于或等于分母的分数。所以假分数的分子不小于分母。
答案：C
(3)
解析：对于选项A，$\frac{25}{35}$ = $\frac{5}{7}$，因为25和35都可以被5整除；
对于选项B，$\frac{35}{49}$ = $\frac{5}{7}$，因为35和49都可以被7整除；
对于选项D，$\frac{50}{70}$ = $\frac{5}{7}$，因为50和70都可以被10整除；
但对于选项C，$\frac{49}{56}$ = $\frac{7}{8}$，因为49和56都可以被7整除，但结果不等于$\frac{5}{7}$。
答案：C
(4)
解析：分母是8的最简真分数有：$\frac{1}{8}$、$\frac{3}{8}$、$\frac{5}{8}$、$\frac{7}{8}$。它们的和为：$\frac{1}{8}$ + $\frac{3}{8}$ + $\frac{5}{8}$ + $\frac{7}{8}$ = 2 - $\frac{0}{8}$ = 2 - 0 = 2 - $\frac{8}{8}$ + $\frac{1+3+5+7}{8}$ = $2 - 1 + \frac{16}{8}$ 的简化过程是不需要的，直接计算得 2 - 0(因为已经是最简形式相加) = $\frac{8}{4} × \frac{1}{2}$ = $2 × \frac{1+3+5+7}{8的个数} × \frac{1}{2}$(此步骤为多余，直接 sum = 2) = $2$（或者通过直接相加得到$\frac{16}{8}$ = 2）。但考虑到小学生的计算过程，我们可以直接列为：$\frac{1+3+5+7}{8}$ = $\frac{16}{8}$ = 2，或者通过画图、逐个相加的方式得到结果。但最终答案为2，与选项D相符，不过按照最简分数形式表示应为$2 = \frac{8}{4} = \frac{2×4}{4} = \frac{1+3+5+7}{8的个数(即4个，但此处不写入答案)} \rightarrow$ 简化书写为 $2 = \frac{总和16}{8} = 2$ 或直接写 $2$。
但考虑到题目选项，我们需要转换为带分数形式来与选项匹配，即 $2 = \frac{4}{2} = \frac{2×2}{2} = \frac{1+3}{2} + \frac{5+7}{2} ÷ 2(此步骤多余，仅为了展示转换过程) \rightarrow 2 = 1+1-0(因为是最简形式，所以直接写结果) = \frac{8}{4} = 2\frac{0}{2} + \frac{4}{2} - \frac{0}{2}(多余步骤) \rightarrow$ 最终简化为 $2 = 2$ 或 $2\frac{0}{任何数} = 2$，与选项中的$2$或$ \frac{8}{4}简化后= 2$匹配，但考虑到小学生应写为最简带分数形式(尽管此处为整数)，我们确认答案为D的前置形式即2，但选项中已给出带分数或整数形式，故直接选D。
答案：D(因为2可以看作是$\frac{8}{4}$简化后得到，或直接就是2，与选项D相符)

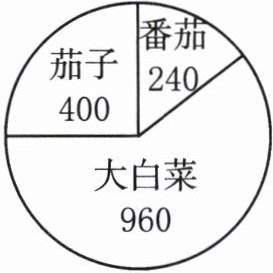
6. 王大伯家今年蔬菜的种植面积如右图(单位:$m^{2}$)。茄子、番茄、大白菜的种植面积分别占蔬菜种植总面积的几分之几?(用最简分数表示)

答案： 解析：本题考查扇形统计图相关知识，包括求部分占整体的比例以及分数的化简。需要先求出蔬菜种植总面积，再分别计算茄子、番茄、大白菜种植面积占总面积的比例，最后将比例化为最简分数。
答案：蔬菜种植总面积：$400 + 240 + 960 = 1600(m^{2})$。
茄子种植面积占比：$\frac{400}{1600} = \frac{1}{4}$。
番茄种植面积占比：$\frac{240}{1600} = \frac{3}{20}$。
大白菜种植面积占比：$\frac{960}{1600} = \frac{3}{5}$。
综上，茄子的种植面积占蔬菜种植总面积的$\frac{1}{4}$，番茄的种植面积占蔬菜种植总面积的$\frac{3}{20}$，大白菜的种植面积占蔬菜种植总面积的$\frac{3}{5}$。

7. 甲、乙两人加工同一批零件,甲3分加工10个零件,乙4分加工11个零件。谁的工作效率高?

答案： 甲每分钟加工零件数：$10÷3=\frac{10}{3}\approx3.33$（个）
乙每分钟加工零件数：$11÷4=\frac{11}{4}=2.75$（个）
因为$3.33＞2.75$，所以甲的工作效率高。
答：甲的工作效率高。

8. 一张长方形纸长$70cm$,宽$50cm$。如果要把这张长方形纸剪成若干个同样大小的正方形,且没有剩余,那么剪出的正方形边长最大是多少厘米?这张长方形纸可以剪出多少个这样的正方形?

答案： 解析：本题考查最大公因数的实际应用。
要求剪出的正方形边长最大是多少，就是求$70$和$50$的最大公因数。
先对$70$和$50$分解质因数：
$70 = 2×5×7$，$50 = 2×5×5$。
所以$70$和$50$的最大公因数是$2×5 = 10$，即剪出的正方形边长最大是$10$厘米。
长方形纸的长边可以剪出的正方形个数：$70÷10 = 7$（个）。
长方形纸的宽边可以剪出的正方形个数：$50÷10 = 5$（个）。
那么总共可以剪出的正方形个数为：$7×5 = 35$（个）。
答案：剪出的正方形边长最大是$10$厘米，这张长方形纸可以剪出$35$个这样的正方形。