第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
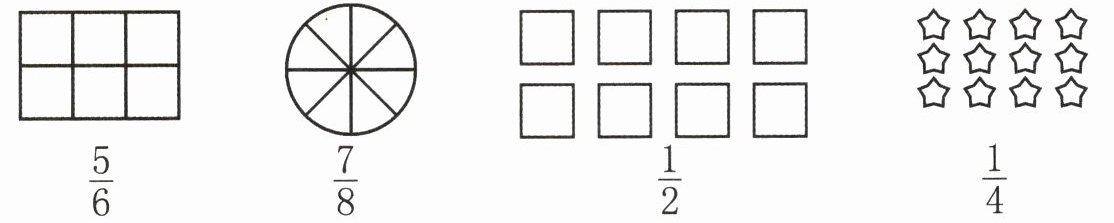
1. 根据下面的分数在各图中涂色。

答案:
本题可根据分数的意义,分别确定各图形中需要涂色的部分数量,进而完成涂色。
1. 对于$\frac{5}{6}$
观察第一个图形,它被平均分成了$6$个小正方形,根据分数的意义,分母表示平均分成的份数,分子表示取的份数,所以$\frac{5}{6}$表示要涂$5$个小正方形。
2. 对于$\frac{7}{8}$
第二个图形是一个圆,被平均分成了$8$份,$\frac{7}{8}$表示要涂其中的$7$份。
3. 对于$\frac{1}{2}$
第三个图形有$8$个小正方形,将其看作一个整体,平均分成$2$份,每份有$8÷2 = 4$个小正方形,$\frac{1}{2}$表示涂其中的$1$份,即涂$4$个小正方形。
4. 对于$\frac{1}{4}$
第四个图形有$12$颗星星,将其看作一个整体,平均分成$4$份,每份有$12÷4 = 3$颗星星,$\frac{1}{4}$表示涂其中的$1$份,即涂$3$颗星星。
综上,第一个图涂$5$个小正方形;第二个图涂$7$份;第三个图涂$4$个小正方形;第四个图涂$3$颗星星。(图略)。
1. 对于$\frac{5}{6}$
观察第一个图形,它被平均分成了$6$个小正方形,根据分数的意义,分母表示平均分成的份数,分子表示取的份数,所以$\frac{5}{6}$表示要涂$5$个小正方形。
2. 对于$\frac{7}{8}$
第二个图形是一个圆,被平均分成了$8$份,$\frac{7}{8}$表示要涂其中的$7$份。
3. 对于$\frac{1}{2}$
第三个图形有$8$个小正方形,将其看作一个整体,平均分成$2$份,每份有$8÷2 = 4$个小正方形,$\frac{1}{2}$表示涂其中的$1$份,即涂$4$个小正方形。
4. 对于$\frac{1}{4}$
第四个图形有$12$颗星星,将其看作一个整体,平均分成$4$份,每份有$12÷4 = 3$颗星星,$\frac{1}{4}$表示涂其中的$1$份,即涂$3$颗星星。
综上,第一个图涂$5$个小正方形;第二个图涂$7$份;第三个图涂$4$个小正方形;第四个图涂$3$颗星星。(图略)。
2. 选择。
(1) 用分数表示下列各图中的阴影部分,正确的是(

(2) 一个正方形的$\frac {1}{4}$是 ,这个正方形的$\frac {3}{4}$是(
,这个正方形的$\frac {3}{4}$是(

(1) 用分数表示下列各图中的阴影部分,正确的是(
A
)。
(2) 一个正方形的$\frac {1}{4}$是
 ,这个正方形的$\frac {3}{4}$是(
,这个正方形的$\frac {3}{4}$是(A
)。
答案:
A,A
3. 在相应的图中表示下面信息里的分数。
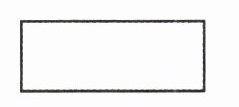
(1) 我们班有$\frac {1}{3}$的同学报名参加书法兴趣班。
(2) 小明生日,每人分到整个蛋糕的$\frac {1}{8}$。
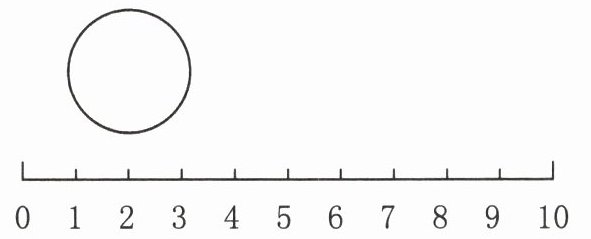
(3) 死海表层的水中含盐量约$\frac {3}{10}$。
(1) 我们班有$\frac {1}{3}$的同学报名参加书法兴趣班。

图中矩形平均分成3份,给其中1份涂色,表示这个矩形的$\frac {1}{3}$。
(2) 小明生日,每人分到整个蛋糕的$\frac {1}{8}$。

图中圆形平均分成8份,给其中1份涂色,表示这个圆形的$\frac {1}{8}$。
(3) 死海表层的水中含盐量约$\frac {3}{10}$。
图中数轴从0到1共10格,将其中3格涂色,表示整个单位的$\frac {3}{10}$。
答案:
(1)图中矩形平均分成3份,给其中1份涂色,表示这个矩形的$\frac {1}{3}$。
(2)图中圆形平均分成8份,给其中1份涂色,表示这个圆形的$\frac {1}{8}$。
(3)图中数轴从0到1共10格,将其中3格涂色,表示整个单位的$\frac {3}{10}$。
(2)图中圆形平均分成8份,给其中1份涂色,表示这个圆形的$\frac {1}{8}$。
(3)图中数轴从0到1共10格,将其中3格涂色,表示整个单位的$\frac {3}{10}$。
4. 淘气有24张贺卡,这些贺卡的$\frac {1}{4}$是(
6
)张。笑笑有36张贺卡,这些贺卡的$\frac {1}{4}$是(9
)张。
答案:
解析:本题考查分数乘法的意义,即求一个数的几分之几是多少用乘法计算。
对于淘气的$24$张贺卡,求它的$\frac{1}{4}$,可列式为$24×\frac{1}{4}$;对于笑笑的$36$张贺卡,求它的$\frac{1}{4}$,可列式为$36×\frac{1}{4}$。
答案:
$24×\frac{1}{4}=6$(张)
$36×\frac{1}{4}=9$(张)
故答案依次为:$6$;$9$。
对于淘气的$24$张贺卡,求它的$\frac{1}{4}$,可列式为$24×\frac{1}{4}$;对于笑笑的$36$张贺卡,求它的$\frac{1}{4}$,可列式为$36×\frac{1}{4}$。
答案:
$24×\frac{1}{4}=6$(张)
$36×\frac{1}{4}=9$(张)
故答案依次为:$6$;$9$。
5. 甲、乙两个工程队各修一条路,甲工程队修了全程的$\frac {1}{7}$,乙工程队也修了全程的$\frac {1}{7}$。甲、乙两个工程队已修的路一样长吗?为什么?
答案:
解析:本题考查分数意义的理解。题目中虽然甲工程队和乙工程队修的路都占各自全程的$\frac{1}{7}$,但是没有明确两条路的全程长度是否相等。如果全程长度不同,即使占比相同,实际修的长度也可能不同。
答案:甲、乙两个工程队已修的路不一定一样长。因为虽然他们都修了各自全程的$\frac{1}{7}$,但两条路的全程长度可能不同,所以已修的路长也可能不同。
答案:甲、乙两个工程队已修的路不一定一样长。因为虽然他们都修了各自全程的$\frac{1}{7}$,但两条路的全程长度可能不同,所以已修的路长也可能不同。
查看更多完整答案,请扫码查看


