《2025年作业本浙江教育出版社五年级数学上册北师大版》

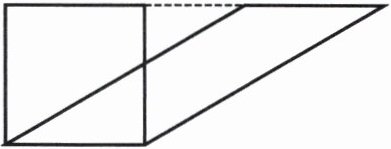
5. 下图中,正方形的周长是24 cm,平行四边形的面积是多少平方厘米?

答案： 解析：本题考查正方形周长公式、平行四边形面积公式的应用。
已知正方形的周长是$24$厘米，根据正方形的周长公式$C = 4a$（$C$表示周长，$a$表示边长），可得正方形的边长为：
$24÷4 = 6$（厘米）
观察图形可知，平行四边形的底等于正方形的边长，平行四边形的高也等于正方形的边长。
根据平行四边形的面积公式$S = ah$（$S$表示面积，$a$表示底，$h$表示高），可得平行四边形的面积为：
$6×6 = 36$（平方厘米）
答案：$36$平方厘米。

6. 一块平行四边形的麦田,底是300 m,高是240 m,共收小麦43200 kg。平均每平方米麦田收小麦多少千克?

答案： 解析：本题考查平行四边形面积以及平均数的计算。
首先，需要计算平行四边形麦田的面积，然后用总收获的小麦重量除以面积，就可以得到平均每平方米收获的小麦重量。
平行四边形的面积计算公式是：面积 = 底 × 高。
根据题目，底是300m，高是240m，所以面积 $S = 300× 240 = 72000(平方米)$。
然后，用总收获的小麦重量43200kg除以面积72000平方米，就可以得到平均每平方米收获的小麦重量。
即：平均每平方米收获的小麦 = 总小麦重量${÷}$麦田面积 $= 43200 {÷}72000 = 0.6(kg)$。
答案：平均每平方米麦田收小麦0.6千克。

7. 木材市场有一些由原木堆成的原木堆。原木堆的横截面是梯形,每堆最上层都有5根原木,相邻的两层,下面一层都比上面一层多1根原木,一共有8层。每堆有原木多少根?

答案： 解析：
本题是一个等差数列求和的问题，其中首项是5，公差是1，项数是8。
我们可以使用等差数列的求和公式来解决这个问题，但考虑到小学生的知识水平，我们也可以通过逐层相加的方式来求解。
即，把每一层的原木数加起来，得到总的原木数。
最上层有5根原木，第二层有$5+1=6(根)$，第三层有$6+1=7(根)$，以此类推，第八层有$5+7 × 1=12(根)$，
所以，原木堆中每层原木数分别为：5根、6根、7根、8根、9根、10根、11根、12根，
接下来，我们将这些原木数加起来，得到总的原木数：
$5+6+7+8+9+10+11+12$
$=(5+12) × 8 ÷ 2$
$=17 × 8 ÷ 2$
$=68$(根)
答案：
每堆有原木68根。

8. 某医院计划用长24 m、宽1.8 m的白布做两条直角边都是0.6 m的救护用的三角巾,可做多少条?

答案： 解析：本题考查了三角形的面积公式在实际生活中的应用，同时涉及到除法的运算。
首先，我们需要计算一个三角巾的面积。
已知三角巾的两条直角边都是$0.6m$，
根据直角三角形的面积公式：面积 = 直角边1 × 直角边2 ÷ 2，
可以计算出单个三角巾的面积：
$0.6 × 0.6 ÷ 2 = 0.18（平方米）$
接下来，我们要计算白布的总面积。
已知白布的长为$24m$，宽为$1.8m$，
根据长方形的面积公式：面积 = 长 × 宽，
可以计算出白布的面积：
$24 × 1.8 = 43.2（平方米）$
然后，我们用白布的总面积除以一个三角巾的面积，就可以得到理论上可以制作的三角巾的数量：
$43.2 ÷ 0.18 = 240（条）$
但是，因为三角巾是不可分割的，所以我们需要取整数部分，即实际可以制作的三角巾的数量。
在这个例子中，$240$条已经是整数，所以不需要进行取整操作。
另外，因为要做两条直角边都是$0.6m$的三角巾，而白布的宽度$1.8m$恰好是$0.6m$的3倍，长度$24m$是$0.6m$的40倍，所以白布可以完整地被划分成很多个$0.6m × 0.6m$的小正方形，每个小正方形又可以切成两个这样的三角巾。
所以，实际上我们可以做的三角巾的数量就是$2 × (24÷0.6) × (1.8÷0.6) = 240（条）$（因为每个小正方形可以做2条三角巾）。
答案：可做$240$条。

9. 求右图中阴影部分的面积。

答案： 大正方形面积：4×4=16(cm²)
小正方形边长：4-2=2(cm)
小正方形面积：2×2=4(cm²)
阴影部分面积：16+16-2×4=24(cm²)
答：阴影部分的面积是24cm²。

*10. 一个三角形的底是9 cm,若高不变,底边延长4 cm,则面积增加$16cm^{2}$。原三角形的面积是多少平方厘米?

答案： 解析：本题可根据三角形面积公式，结合底边延长后面积增加的条件，先求出三角形的高，再计算原三角形的面积。
步骤一：求出三角形的高
设原三角形的高为$h$厘米。
根据三角形面积公式$S = \frac{1}{2}ah$（其中$S$表示面积，$a$表示底，$h$表示高），原三角形底是$9$厘米，则原三角形面积为$\frac{1}{2}×9× h=\frac{9}{2}h$平方厘米。
底边延长$4$厘米后，新底为$9 + 4 = 13$厘米，此时新三角形面积为$\frac{1}{2}×13× h=\frac{13}{2}h$平方厘米。
已知底边延长后面积增加$16$平方厘米，可据此列出方程：
$\frac{13}{2}h-\frac{9}{2}h = 16$
化简方程左边可得：
$\frac{13}{2}h-\frac{9}{2}h=\frac{13h - 9h}{2}=\frac{4h}{2}=2h$
则方程变为$2h = 16$，解得$h = 8$厘米。
步骤二：计算原三角形的面积
将$h = 8$代入原三角形面积公式$\frac{9}{2}h$，可得原三角形面积为：
$\frac{9}{2}×8 = 36$（平方厘米）
答案：原三角形的面积是$36$平方厘米。