《2025年作业本浙江教育出版社五年级数学上册北师大版》

1. 找出最简分数,在括号里画“√”,并把其余的分数约成最简分数,写在括号里。
$\frac {12}{15}$($\frac{4}{5}$) $\frac {5}{36}$(√) $\frac {36}{60}$($\frac{3}{5}$) $\frac {49}{56}$($\frac{7}{8}$) $\frac {16}{35}$(√)
$\frac {22}{100}$($\frac{11}{50}$) $\frac {7}{16}$(√) $\frac {24}{45}$($\frac{8}{15}$) $\frac {28}{18}$($\frac{14}{9}$) $\frac {40}{12}$($\frac{10}{3}$)

答案： $\frac{12}{15}$($\frac{4}{5}$) $\frac{5}{36}$(√) $\frac{36}{60}$($\frac{3}{5}$) $\frac{49}{56}$($\frac{7}{8}$) $\frac{16}{35}$(√)
$\frac{22}{100}$($\frac{11}{50}$) $\frac{7}{16}$(√) $\frac{24}{45}$($\frac{8}{15}$) $\frac{28}{18}$($\frac{14}{9}$) $\frac{40}{12}$($\frac{10}{3}$)

2. 连一连。

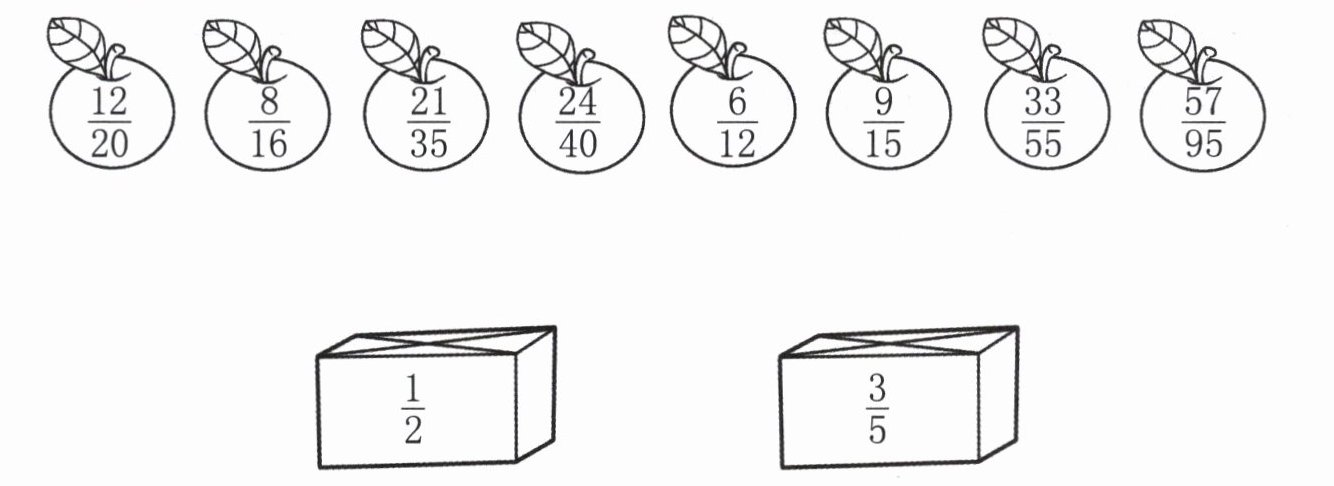
答案： 对上面一排分数进行约分：
$\frac{12}{20}=\frac{3}{5}$；
$\frac{8}{16}=\frac{1}{2}$；
$\frac{21}{35}=\frac{3}{5}$；
$\frac{24}{40}=\frac{3}{5}$；
$\frac{6}{12}=\frac{1}{2}$；
$\frac{9}{15}=\frac{3}{5}$；
$\frac{33}{55}=\frac{3}{5}$；
$\frac{57}{95}=\frac{3}{5}$。
约分后，将分数与下面相应的盒子进行连线即可。

3. 在$◯$里填“$＞$”“$＜$”或“$=$”。
$\frac {7}{4}◯$＜$\frac {10}{3}$ $\frac {5}{6}◯$＞$\frac {2}{3}$ $\frac {3}{4}◯$=$\frac {18}{24}$ $\frac {8}{16}◯$＞$\frac {4}{32}$ $\frac {24}{16}◯$=$\frac {15}{10}$

答案： 解析：本题考查的是分数之间的大小比较。当分数的分母不同时，需要通分或者将分数化为小数来比较大小，也可以根据分数的性质，如交叉相乘等方法进行比较。
答案：
$\frac{7}{4} ＜ \frac{10}{3}$；
$\frac{5}{6} ＞ \frac{2}{3}$；
$\frac{3}{4} = \frac{18}{24}$；
$\frac{8}{16} ＞ \frac{4}{32}$；
$\frac{24}{16} = \frac{15}{10}$。

4. 草地上有40只鸡,其中母鸡有24只,公鸡有16只。请用最简分数表示母鸡、公鸡的只数分别占母鸡和公鸡总数的几分之几。

答案： 解析：
本题考查的是用分数表示一个数是另一个数的几分之几，以及最简分数的表示。
首先，我们知道草地上总共有40只鸡，其中母鸡有24只，公鸡有16只。
接下来，我们要找出母鸡和公鸡分别占总数的几分之几，并用最简分数来表示。
对于母鸡：
母鸡的数量是24，总数是40。
所以，母鸡占总数的比例为 $\frac{24}{40}$。
为了得到最简分数，我们需要对分子和分母进行约分。
24和40的最大公约数是8，所以：
$\frac{24}{40} = \frac{24 ÷ 8}{40 ÷ 8} = \frac{3}{5}$
对于公鸡：
公鸡的数量是16，总数是40。
所以，公鸡占总数的比例为 $\frac{16}{40}$。
同样地，为了得到最简分数，我们需要对分子和分母进行约分。
16和40的最大公约数是8，所以：
$\frac{16}{40} = \frac{16 ÷ 8}{40 ÷ 8} = \frac{2}{5}$
答案：
母鸡占总数的比例为 $\frac{3}{5}$，公鸡占总数的比例为 $\frac{2}{5}$。

5. 在一次跑步比赛中,淘气10秒跑了75m,笑笑8秒跑了60m。谁跑得快？为什么？

答案： 解析：本题考查的是路程，速度和时间的关系。通过比较两者的速度来判断谁跑得快。
速度可以通过路程除以时间来计算，即：速度 = 路程 ÷ 时间。
淘气的速度为：
75 ÷ 10 = 7.5（米/秒）；
笑笑的速度为：
60 ÷ 8 = 7.5（米/秒）。
7.5米/秒=7.5米/秒，即淘气的速度和笑笑的速度一样。
答案：淘气和笑笑跑得一样快，因为他们每秒都跑了7.5米。

6. 在图中表示下列分数,你发现了什么？
$\frac {4}{6}$ $1\frac {1}{3}$ $\frac {10}{12}$ $\frac {5}{6}$ $\frac {12}{9}$ $\frac {8}{12}$

答案： 解析：本题主要考查在数轴上表示分数以及约分的知识点。在数轴上表示分数时，需要先确定每个分数所对应的刻度位置。对于$\frac{4}{6}$，可化简为$\frac{2}{3}$；$1\frac{1}{3}$是带分数，可写成$\frac{4}{3}$；$\frac{10}{12}$化简后为$\frac{5}{6}$；$\frac{12}{9}$化简后为$\frac{4}{3}$；$\frac{8}{12}$化简后为$\frac{2}{3}$。通过化简可以发现，$\frac{4}{6}$和$\frac{8}{12}$、$\frac{10}{12}$和$\frac{5}{6}$、$1\frac{1}{3}$和$\frac{12}{9}$分别相等。
答案：$\frac{4}{6}=\frac{2}{3}$，在数轴上将$0$到$1$这一段平均分成$3$份，取其中的$2$份处标记$\frac{4}{6}$；
$1\frac{1}{3}=\frac{4}{3}$，在数轴上从$1$开始，将$1$到$2$这一段平均分成$3$份，取其中的$1$份处标记$1\frac{1}{3}$；
$\frac{10}{12}=\frac{5}{6}$，在数轴上将$0$到$1$这一段平均分成$6$份，取其中的$5$份处标记$\frac{10}{12}$；
$\frac{5}{6}$，在数轴上将$0$到$1$这一段平均分成$6$份，取其中的$5$份处标记$\frac{5}{6}$；
$\frac{12}{9}=\frac{4}{3}$，在数轴上从$1$开始，将$1$到$2$这一段平均分成$3$份，取其中的$1$份处标记$\frac{12}{9}$；
$\frac{8}{12}=\frac{2}{3}$，在数轴上将$0$到$1$这一段平均分成$3$份，取其中的$2$份处标记$\frac{8}{12}$。
发现：$\frac{4}{6}=\frac{8}{12}=\frac{2}{3}$，$\frac{10}{12}=\frac{5}{6}$，$1\frac{1}{3}=\frac{12}{9}=\frac{4}{3}$ ，即化简后相等的分数在数轴上对应同一点。