《2025年作业本浙江教育出版社五年级数学上册北师大版》

9. 选择合适的数填一填。
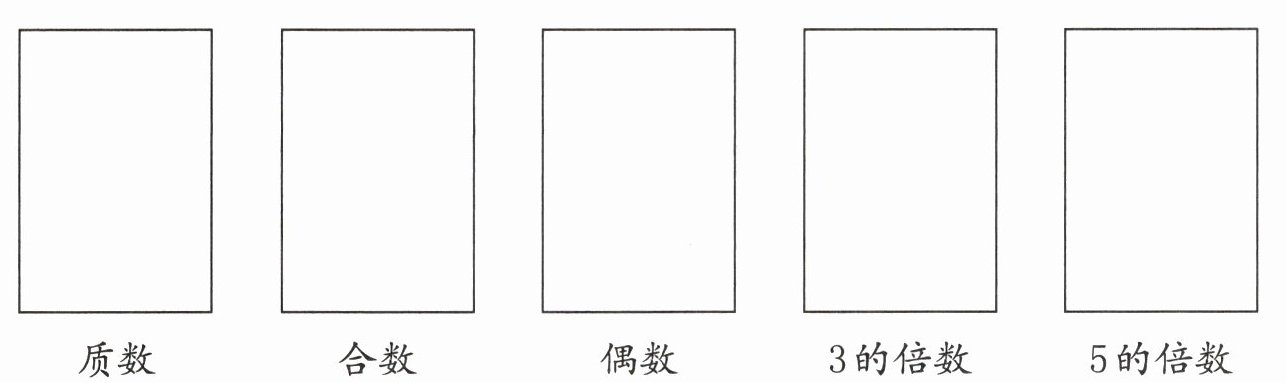
45 4 97 1 18 212 240 57 66 13 63

答案： 质数：97，13
合数：45，4，18，212，240，57，66，63
偶数：4，18，212，240，66
3的倍数：45，18，240，57，66，63
5的倍数：45，240

10. 每千克辣椒含维生素C约2g,每千克橙子含维生素C约0.55g。每千克辣椒中维生素C的含量大约是橙子的几倍?(结果保留一位小数)

答案： 解析：本题考查的是利用除法运算来解决实际问题，具体是求一个数是另一个数的几倍，用除法计算，同时要按照题目要求对结果保留一位小数。
答案：$2÷0.55\approx3.6$
答：每千克辣椒中维生素$C$的含量大约是橙子的$3.6$倍。

11. 买4个小恐龙玩具和2个小汽车玩具需要46.60元,买4个小恐龙玩具和5个小汽车玩具需要66.10元。一个小恐龙玩具需要多少元?一个小汽车玩具呢?

答案： 解析：本题可通过设未知数，根据已知条件列出方程组，进而求解一个小恐龙玩具和一个小汽车玩具的价格。
设一个小恐龙玩具的价格为$x$元，一个小汽车玩具的价格为$y$元。
步骤一：根据已知条件列方程组
已知买$4$个小恐龙玩具和$2$个小汽车玩具需要$46.60$元，可列方程$4x + 2y = 46.6$ ①；
买$4$个小恐龙玩具和$5$个小汽车玩具需要$66.10$元，可列方程$4x + 5y = 66.1$ ②。
步骤二：消元求解$y$的值
用方程②减去方程①，可得：
$(4x + 5y) - (4x + 2y) = 66.1 - 46.6$
去括号得：$4x + 5y - 4x - 2y = 19.5$
合并同类项得：$3y = 19.5$
两边同时除以$3$，解得：$y = 6.5$
步骤三：将$y$的值代入方程求解$x$的值
把$y = 6.5$代入方程①$4x + 2×6.5 = 46.6$，即$4x + 13 = 46.6$。
方程两边同时减去$13$得：$4x = 46.6 - 13 = 33.6$。
两边再同时除以$4$，解得：$x = 8.4$。
答案：一个小恐龙玩具需要$8.4$元，一个小汽车玩具需要$6.5$元。

*12. $1÷7$的商的小数部分第100位上的数字是几?这100个数字之和是多少?

答案： 解析：
本题考查循环小数的特征。
$1÷ 7=0.\dot{1}4285\dot{7}$，循环节是$142857$，有$6$个数字。
用$100$除以循环节的位数：
$100 ÷ 6 = 16\dots 4$。
因为余数是$4$，
所以第$100$位上的数字是循环节的第$4$个数字，即$8$。
每个循环节的数字之和是：
$1 + 4 + 2 + 8 + 5 + 7 = 27$。
因为有$16$个完整的循环节，
所以这$16$个循环节的数字之和是：
$16 × 27 = 432$。
还需要加上余下的$4$个数字，
即第$100$位之前的$4$个数字：$1 + 4 + 2 + 8 = 15$。
所以，前$100$个数字的总和是：
$432 + 15 = 447$。
答：第$100$位上的数字是$8$，这$100$个数字之和是$447$。