第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
|图形|三角形|三角形|三角形|三角形|平行四边形|平行四边形|
|底/cm|4|
|高/cm|2.4|7|
|面积$/cm^2$|
|底/cm|4|
1
|2.5|9|3
|3||高/cm|2.4|7|
4.8
|6.5|2.7
|2.7
||面积$/cm^2$|
4.8
|3.5|6|29.25
|8.1
|8.1|
答案:
解析:本题考查三角形和平行四边形面积的计算。需要根据给定的底和高(或面积)来计算缺失的数值。
三角形的面积公式是:$面积 = \frac{1}{2} × 底 × 高$,
平行四边形的面积公式是:$面积 = 底 × 高$,
对于三角形:
第一个三角形:底是4cm,高是2.4cm。
$面积 = \frac{1}{2} × 4 × 2.4 = 4.8 (cm^2)$;
第二个三角形:面积是3.5$cm^2$,高是7cm。
$底 = \frac{2 × 面积}{高} = \frac{2 × 3.5}{7} = 1(cm)$;
第三个三角形:底是2.5cm,面积是6$cm^2$。
$高 = \frac{2 × 面积}{底} = \frac{2 × 6}{2.5} = 4.8(cm)$;
第四个三角形:底是9cm,高是6.5cm。
$面积 = \frac{1}{2} × 9 × 6.5 = 29.25 (cm^2)$;
对于平行四边形:
第一个平行四边形:底是3cm,面积是8.1$cm^2$。
$高 = \frac{面积}{底} = \frac{8.1}{3} = 2.7(cm)$;
答案:$4.8$;$1$;$4.8$;$29.25$;$3$;$2.7$。
三角形的面积公式是:$面积 = \frac{1}{2} × 底 × 高$,
平行四边形的面积公式是:$面积 = 底 × 高$,
对于三角形:
第一个三角形:底是4cm,高是2.4cm。
$面积 = \frac{1}{2} × 4 × 2.4 = 4.8 (cm^2)$;
第二个三角形:面积是3.5$cm^2$,高是7cm。
$底 = \frac{2 × 面积}{高} = \frac{2 × 3.5}{7} = 1(cm)$;
第三个三角形:底是2.5cm,面积是6$cm^2$。
$高 = \frac{2 × 面积}{底} = \frac{2 × 6}{2.5} = 4.8(cm)$;
第四个三角形:底是9cm,高是6.5cm。
$面积 = \frac{1}{2} × 9 × 6.5 = 29.25 (cm^2)$;
对于平行四边形:
第一个平行四边形:底是3cm,面积是8.1$cm^2$。
$高 = \frac{面积}{底} = \frac{8.1}{3} = 2.7(cm)$;
答案:$4.8$;$1$;$4.8$;$29.25$;$3$;$2.7$。
2. 在下面的方格纸上分别画两个三角形,一个三角形的面积与左边三角形的面积相等,另一个三角形的面积等于左边三角形面积的一半。


答案:
解析:本题考查的知识点是三角形的面积公式以及等面积三角形和面积减半三角形的绘制。需要利用三角形面积公式$S = \frac{1}{2}ah$($a$为底,$h$为高),通过保持底和高的乘积不变来绘制等面积三角形,通过底和高的乘积减半来绘制面积减半三角形。
答案:图略(提示:第一个三角形,底为$4$格,高为$3$格;第二个三角形,底为$2$格,高为$3$格,位置可自由选择)。
答案:图略(提示:第一个三角形,底为$4$格,高为$3$格;第二个三角形,底为$2$格,高为$3$格,位置可自由选择)。
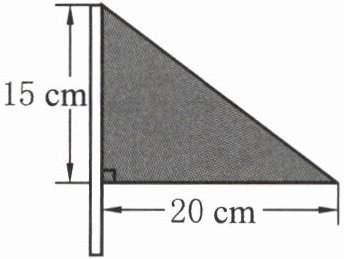
3. 学校开运动会,五(1)班同学准备制作啦啦队用的小彩旗,如右图,做50面这样的小彩旗至少要用多少平方厘米彩纸?

答案:
解析:本题考查了三角形面积公式的应用。
先根据三角形面积公式求出一面小彩旗的面积,再乘以$50$,即可求出做$50$面这样的小彩旗至少要用多少平方厘米彩纸。
三角形的面积公式为:$面积 =\frac{1}{2} × 底 × 高$,将底边$20$厘米和高$15$厘米代入公式,可得一面小彩旗的面积为:
$\frac{1}{2} × 20 × 15$
$= 10× 15$
$= 150$(平方厘米)
则$50$面小彩旗的面积为:$150 × 50 = 7500$(平方厘米)。
答案:7500平方厘米。
先根据三角形面积公式求出一面小彩旗的面积,再乘以$50$,即可求出做$50$面这样的小彩旗至少要用多少平方厘米彩纸。
三角形的面积公式为:$面积 =\frac{1}{2} × 底 × 高$,将底边$20$厘米和高$15$厘米代入公式,可得一面小彩旗的面积为:
$\frac{1}{2} × 20 × 15$
$= 10× 15$
$= 150$(平方厘米)
则$50$面小彩旗的面积为:$150 × 50 = 7500$(平方厘米)。
答案:7500平方厘米。
4. 如右图,笑笑用一张长80 cm、宽30 cm的长方形卡纸剪直角三角形,一共可以剪多少个这样的三角形?


答案:
解析:本题考查长方形面积公式和三角形面积公式的实际应用,可先算出长方形卡纸能剪出多少个长$20\text{cm}$、宽$15\text{cm}$的小长方形,再根据每个小长方形可剪成两个符合要求的直角三角形,进而求出直角三角形的个数。
长方形的面积公式为$S = a× b$(其中$S$为长方形面积,$a$为长方形的长,$b$为长方形的宽)。
已知长方形卡纸长$80\text{cm}$、宽$30\text{cm}$,则长方形卡纸的面积为:
$80×30 = 2400$($\text{cm}^2$)。
每个小直角三角形的底是$20\text{cm}$、高是$15\text{cm}$,根据三角形的面积公式$S = \frac{1}{2}× a× h$(其中$S$为三角形面积,$a$为三角形的底,$h$为三角形的高),可得每个小直角三角形的面积为:
$\frac{1}{2}×20×15 = 150$($\text{cm}^2$)。
每个长$20\text{cm}$、宽$15\text{cm}$的小长方形可剪成两个这样的直角三角形,那么每个小长方形的面积为:
$20×15 = 300$($\text{cm}^2$)。
长方形卡纸的长$80\text{cm}$包含$20\text{cm}$的个数为:
$80÷20 = 4$(个)。
长方形卡纸的宽$30\text{cm}$包含$15\text{cm}$的个数为:
$30÷15 = 2$(个)。
则能剪出长$20\text{cm}$、宽$15\text{cm}$的小长方形的个数为:
$4×2 = 8$(个)。
因为每个小长方形可剪成$2$个直角三角形,所以一共可以剪的直角三角形个数为:
$8×2 = 16$(个)。
答案:一共可以剪$16$个这样的三角形。
长方形的面积公式为$S = a× b$(其中$S$为长方形面积,$a$为长方形的长,$b$为长方形的宽)。
已知长方形卡纸长$80\text{cm}$、宽$30\text{cm}$,则长方形卡纸的面积为:
$80×30 = 2400$($\text{cm}^2$)。
每个小直角三角形的底是$20\text{cm}$、高是$15\text{cm}$,根据三角形的面积公式$S = \frac{1}{2}× a× h$(其中$S$为三角形面积,$a$为三角形的底,$h$为三角形的高),可得每个小直角三角形的面积为:
$\frac{1}{2}×20×15 = 150$($\text{cm}^2$)。
每个长$20\text{cm}$、宽$15\text{cm}$的小长方形可剪成两个这样的直角三角形,那么每个小长方形的面积为:
$20×15 = 300$($\text{cm}^2$)。
长方形卡纸的长$80\text{cm}$包含$20\text{cm}$的个数为:
$80÷20 = 4$(个)。
长方形卡纸的宽$30\text{cm}$包含$15\text{cm}$的个数为:
$30÷15 = 2$(个)。
则能剪出长$20\text{cm}$、宽$15\text{cm}$的小长方形的个数为:
$4×2 = 8$(个)。
因为每个小长方形可剪成$2$个直角三角形,所以一共可以剪的直角三角形个数为:
$8×2 = 16$(个)。
答案:一共可以剪$16$个这样的三角形。
*5. 右图中平行四边形的面积是$36 m^2,A$是底边的中点,求阴影部分的面积。


答案:
设平行四边形的底为$b$,高为$h$,则平行四边形面积$S = b× h = 36\space m^2$。
因为$A$是底边中点,所以阴影三角形的底为$\frac{b}{2}$,高与平行四边形高相同为$h$。
阴影部分面积$S_{\text{阴影}}=\frac{1}{2}×\frac{b}{2}× h=\frac{1}{4}× b× h$。
又因为$b× h = 36\space m^2$,所以$S_{\text{阴影}}=\frac{1}{4}×36 = 9\space m^2$。
答案:$9\space m^2$
因为$A$是底边中点,所以阴影三角形的底为$\frac{b}{2}$,高与平行四边形高相同为$h$。
阴影部分面积$S_{\text{阴影}}=\frac{1}{2}×\frac{b}{2}× h=\frac{1}{4}× b× h$。
又因为$b× h = 36\space m^2$,所以$S_{\text{阴影}}=\frac{1}{4}×36 = 9\space m^2$。
答案:$9\space m^2$
查看更多完整答案,请扫码查看


