《2025年作业本浙江教育出版社五年级数学上册北师大版》

1. 如右图,两个完全相同的梯形能拼成一个底是5cm、高是4cm的平行四边形。原梯形的面积是10$cm^2。$

答案： 解析：本题可根据两个完全相同的梯形拼成平行四边形的特点，先求出拼成的平行四边形的面积，再通过平行四边形与梯形面积的关系求出梯形的面积。
两个完全相同的梯形拼成一个平行四边形，那么平行四边形的面积就是梯形面积的$2$倍。
已知拼成的平行四边形的底是$5cm$、高是$4cm$，根据平行四边形的面积公式$S = a× h$（其中$S$表示面积，$a$表示底，$h$表示高），可得平行四边形的面积为：
$5×4 = 20$（$cm^2$）
因为平行四边形的面积是梯形面积的$2$倍，所以梯形的面积为平行四边形面积的一半，即：
$20÷2 = 10$（$cm^2$）
答案：$10$。

2. 计算下列各图形的面积。(单位:cm)

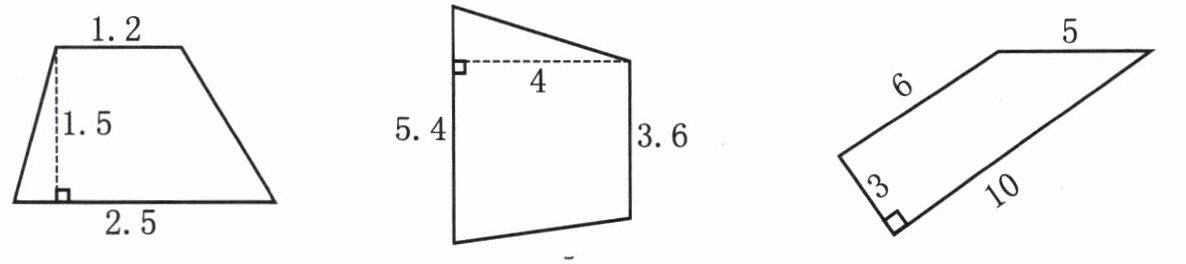
答案： 第一个图形（梯形）：
$面积=(上底+下底)× 高 ÷ 2$，
$=(1.2+2.5)× 1.5 ÷ 2$，
$=3.7× 1.5 ÷ 2$，
$=5.55 ÷ 2$，
$=2.775$（$cm^2$），
第二个图形（直角梯形）：
$面积=(上底+下底)× 高 ÷ 2$，
$=(3.6+5.4)× 4 ÷ 2$，
$=9× 4 ÷ 2$，
$=36 ÷ 2$，
$=18$（$cm^2$），
第三个图形（平行四边形与直角三角形的组合）：
平行四边形的面积：
$底 × 高=6 × 3=18$（$cm^2$），
直角三角形的面积：
$\frac{1}{2} × 底 × 高=\frac{1}{2} × (10-5) × 3=\frac{1}{2} × 5 × 3=7.5$（$cm^2$），
组合图形的面积：
$平行四边形的面积+直角三角形的面积=18+7.5=25.5$（$cm^2$），
综上，第一个图形面积为$2.775cm^2$；第二个图形面积为$18cm^2$；第三个图形面积为$25.5cm^2$。

3. 如右图,一条水渠的横截面是梯形,渠口宽2.4m,渠底宽1.2m,渠深1.2m。这个水渠横截面的面积是多少平方米?

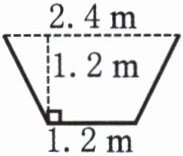
答案： 梯形面积公式：（上底 + 下底）× 高 ÷ 2
上底 = 2.4m，下底 = 1.2m，高 = 1.2m
面积 = （2.4 + 1.2）× 1.2 ÷ 2 = 3.6 × 1.2 ÷ 2 = 4.32 ÷ 2 = 2.16（平方米）
答：这个水渠横截面的面积是2.16平方米。

4. 钢管厂的仓库中有一堆钢管(如右图),请你列式计算这堆钢管的根数。

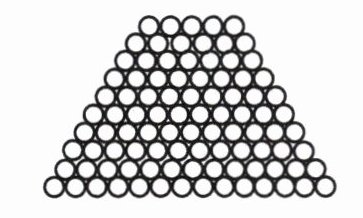
答案： 解：观察图形可知，最上层有$5$根，最下层有$12$根，层数是$12 - 5 + 1 = 8$（层）。
根据梯形面积公式$S=(a + b)h÷2$（这里$a$表示上层根数，$b$表示下层根数，$h$表示层数），可得这堆钢管的根数为$(5 + 12)×8÷2$
$=17×8÷2$
$=136÷2$
$ = 68$（根）。
综上，这堆钢管有$68$根。

5. 一个梯形的上底是10cm,下底是15cm,面积是$200cm^2。$它的高是多少厘米?

答案： 解析：本题可根据梯形的面积公式来求解梯形的高。梯形的面积公式为$S=(a + b)h÷2$（其中$S$表示梯形的面积，$a$表示梯形的上底，$b$表示梯形的下底，$h$表示梯形的高），通过已知的梯形面积、上底和下底，对面积公式进行变形来计算高。
答案：
解：设梯形的高是$x$厘米。
根据梯形面积公式可得方程$(10 + 15)x÷2 = 200$。
$(10 + 15)x÷2×2 = 200×2$
$25x = 400$
$25x÷25 = 400÷25$
$x = 16$
答：它的高是$16$厘米。