《2025年通城学典课时作业本六年级数学上册苏教版》

1. 求下面图形的体积。
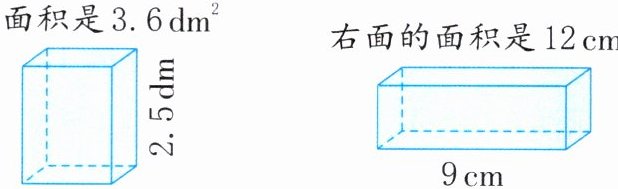
底面积是$3.6dm^2$右面的面积是$12cm^2$

答案： 3.6×2.5=9(dm³) 12×9=108(cm³)

(1)将6立方分米的水倒入一个长方体玻璃容器中(玻璃的厚度忽略不计),如果要计算容器中水面的高度,那么需要知道这个长方体玻璃容器的( )。

A.底面积
B.侧面积
C.表面积
D.体积

答案：
(1)A

(2)一个长方体的底面积和高都扩大为原来的3倍,体积扩大为原来的( )。

A.3倍
B.9倍
C.27倍
D.6倍

答案：
(2)B

3. 一根长为2m的长方体木条,横截面是边长为5cm的正方形。制作400根这样的木条需要木材多少立方米？

答案： 5 cm=0.05 m 2×0.05×0.05×400=2(m³)

4.(名校真题)淘气用橡皮泥做了一个棱长为4厘米的正方体,若把它捏成一个高为2厘米的长方体,则长方体的底面积是多少平方厘米？

答案： 4×4×4=64(立方厘米) 64÷2=32(平方厘米)

5.(传统文化)《天工开物》中记载了用竹子造纸的具体方法,用这种方法造出的竹纸深受人们的喜爱。
(1)“荡料入帘”时,要把煮烂的竹浆倒入长方体造纸槽中。造纸槽内部底面积为$120dm^2,$深5dm,则这个造纸槽最多能装下( )L竹浆。
(2)烘干后的竹纸每100张大约厚1cm,按“三尺斗方(55cm×50cm)”裁切后,平铺在尺寸正好合适的木盒中。若木盒的容积为16500mL,则它最多能装下多少张竹纸？

答案：
(1)600
(2)16500 mL=16500 cm³
16500÷(55×50)=6(cm) 6÷1×100=600(张)

6.(易错题)如图,把一根长1.5米的长方体木料截成两段,这两段木料的表面积总和比原木料的表面积增加了0.36平方米。原来长方体木料的体积是多少立方米？

答案： 0.36÷2×1.5=0.27(立方米) 易错分析:易忽略截成两段,截了一次,相较原木料增加了两个截面的面积,可以先求一个截面的面积,再求体积。

7. 有一个体积是576立方厘米的长方体,前面的面积是96平方厘米,右面的面积是48平方厘米,底面的面积是( )平方厘米。

答案： 72 解析:长方体的体积÷前面的面积=宽,长方体的体积÷右面的面积=长,长方体的底面积=长×宽,列式计算为(576÷48)×(576÷96)=72(平方厘米)。