《2025年通城学典课时作业本六年级数学上册苏教版》

(1)乘积是( )的两个数互为倒数。

答案： 1

(2)( )没有倒数,最小的合数的倒数是( )。

答案： 0 $\frac{1}{4}$

(3)在括号里写出每个数的倒数。
$\frac{7}{9}$( ) $\frac{1}{100}$( ) $1\frac{1}{11}$( )
0.8( ) 1( ) 1.4( )
我发现：当$a＞1$时,$a$的倒数( )1；当$a= 1$时,$a$的倒数( )1；当$0＜a＜1$时,$a$的倒数( )1。(填“＞”“＜”或“=”)

答案： $\frac{9}{7}$ 100 $\frac{11}{12}$ 1.25 1 $\frac{5}{7}$ ＜ = ＞

(4)若$a×\frac{3}{4}= b×2.5= 0.66× c= 1$,则$a$、$b$、$c$中最大的数是( )。

答案： c

(1)因为$\frac{4}{5}×\frac{5}{4}= 1$,所以( )。

A.$\frac{4}{5}$是倒数
B.$\frac{4}{5}和\frac{5}{4}$都是倒数
C.$\frac{5}{4}$是倒数
D.$\frac{4}{5}和\frac{5}{4}$互为倒数

答案： D

(2)(名校真题)真分数的倒数( )比假分数的倒数大。

A.可能
B.一定
C.一定不
D.无法确定

答案： B

(3)(数形结合)下面四幅图中的$a和b$表示不同的数,( )中的$a和b$互为倒数。

三角形的面积为1 线段的总长度为1

A.
B.长方形的面积为1 长方体的体积为1
C.
D.

答案： C

3.(生活应用)有一个棱长是$\frac{4}{5}$分米的正方体纸盒,包装这个纸盒至少需要多少平方分米的包装纸？这个纸盒所占空间有多大？

答案： 包装纸：$\frac{4}{5} × \frac{4}{5} × 6 = \frac{96}{25}$（平方分米）所占空间：$\frac{4}{5} × \frac{4}{5} × \frac{4}{5} = \frac{64}{125}$（立方分米）

4.(传统文化)竹编是我国传统民间手工艺术之一,也是苏州非物质文化遗产项目之一。现用一根$\frac{9}{10}$米长的竹条制作一个小竹篮。
(1)如果还剩$\frac{1}{3}$,那么还剩多少米？
(2)如果用去了$\frac{1}{3}$米,那么还剩多少米？

答案： （1）$\frac{9}{10} × \frac{1}{3} = \frac{3}{10}$（米） （2）$\frac{9}{10} - \frac{1}{3} = \frac{17}{30}$（米）

5. 两个自然数的倒数之和是$\frac{7}{12}$,这两个自然数可能是( )和( ),也可能是( )和( )。

答案： 12 2 3 4

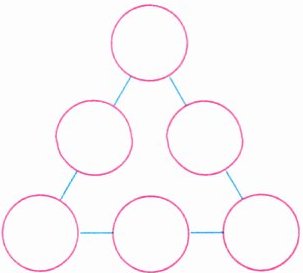
6. 把$\frac{10}{7}$、$\frac{3}{2}$、$\frac{7}{8}$、$\frac{4}{5}$、$\frac{7}{15}$、$\frac{16}{21}$这六个数填入○里,使三角形每条边上三个数的乘积都是1。

答案：

解析：“乘积是1”说明三个数的分子与分母正好全部约去，可以从特殊数开始凑，$\frac{4}{5}$的“4”和$\frac{7}{8}$的“8”可以约分，$\frac{7}{8}$的“7”可以和$\frac{10}{7}$的“7”约分，得到第一道算式：$\frac{4}{5} × \frac{7}{8} × \frac{10}{7} = 1$；$\frac{16}{21}$的分子“16”可以和$\frac{3}{2}$的分母“2”、$\frac{7}{8}$的分母“8”约分，得到第二道算式：$\frac{16}{21} × \frac{3}{2} × \frac{7}{8} = 1$；还剩$\frac{7}{15}$，可得第三道算式：$\frac{10}{7} × \frac{7}{15} × \frac{3}{2} = 1$。三道算式中重复使用的数放在三角形的顶点处，然后根据算式填写剩下的数。