《2025年通城学典课时作业本六年级数学上册苏教版》

(1)(名校真题)冬冬家有一块$\frac{1}{2}$公顷的土地,用它的$\frac{3}{5}$来种土豆。请你帮他算一算,种土豆的面积是多少公顷？
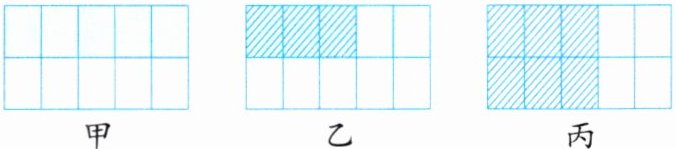
① 冬冬用一个大长方形表示1公顷,画出了解决这个问题的示意图,你认为冬冬画的图( )能表示解决这个问题的思考过程。
甲 乙 丙

② 列式计算：______

答案： ①本题可根据分数乘法的意义，结合题目中土地面积和种土豆所占比例来分析示意图。
已知冬冬家有一块$\frac{1}{2}$公顷的土地，用它的$\frac{3}{5}$来种土豆。
甲图：将大长方形平均分成$10$份，阴影部分占$3$份，可看作先将大长方形看作$1$公顷，先取其中的$\frac{1}{2}$（即$5$份），再从这$\frac{1}{2}$中取$\frac{3}{5}$（$3$份），符合$\frac{1}{2}$公顷的$\frac{3}{5}$的意义。
乙图：将大长方形平均分成$10$份，阴影部分占$5$份中的$3$份，其表示的意义不符合本题$\frac{1}{2}$公顷的$\frac{3}{5}$。
丙图：将大长方形平均分成$6$份，阴影部分占$3$份，其表示的意义不符合本题$\frac{1}{2}$公顷的$\frac{3}{5}$。
所以，冬冬画的图甲能表示解决这个问题的思考过程。
②本题可根据求一个数的几分之几是多少用乘法计算来列式求解。
已知土地面积是$\frac{1}{2}$公顷，种土豆的面积占这块地的$\frac{3}{5}$，则种土豆的面积为：
$\frac{1}{2}×\frac{3}{5}=\frac{3}{10}$（公顷）
本题填：$\frac{1}{2}×\frac{3}{5}=\frac{3}{10}$（公顷）。

(2)在括号里填合适的数。
$\frac{1}{4}$日= ( )时 $\frac{5}{16}$升= ( )毫升
$2\frac{13}{20}dm^3$= ( )$dm^3$( )$cm^3$

答案： 解析：
本题考查的是单位换算的知识点，涉及到日与小时、升与毫升、立方分米与立方厘米之间的换算。
1日 = 24小时，所以 $\frac{1}{4}$日 = $\frac{1}{4}$ × 24 = 6小时。
1升 = 1000毫升，所以 $\frac{5}{16}$升 = $\frac{5}{16}$ × 1000 = 312.5毫升。
1立方分米(dm³) = 1000立方厘米(cm³)，
所以 $2\frac{13}{20}$dm³ = 2dm³ + $\frac{13}{20}$dm³ = 2dm³ + $\frac{13}{20}$ × 1000cm³ = 2dm³650cm³。
答案：
6；312.5；2；650

(3)在○里填“＞”“＜”或“=”。($a＞0$)
$\frac{11}{12}×\frac{8}{9}$○$\frac{11}{12}×\frac{2}{7}$ $\frac{7}{8}×\frac{11}{9}$○$\frac{7}{8}×\frac{5}{3}$
$\frac{2}{9}×\frac{a}{5}$○$\frac{a}{9}×\frac{2}{5}$ $\frac{2}{3}×\frac{4}{a}$○$\frac{1}{a}×\frac{8}{9}$

答案： $\frac{11}{12}×\frac{8}{9}$＞$\frac{11}{12}×\frac{2}{7}$；$\frac{7}{8}×\frac{11}{9}$＜$\frac{7}{8}×\frac{5}{3}$；$\frac{2}{9}×\frac{a}{5}$=$\frac{a}{9}×\frac{2}{5}$；$\frac{2}{3}×\frac{4}{a}$＞$\frac{1}{a}×\frac{8}{9}$

2. 计算下面各题。
$60×\frac{3}{2}×\frac{7}{9}$ $\frac{3}{4}×\frac{8}{7}×\frac{14}{15}$
$\frac{12}{5}×\frac{3}{8}×\frac{5}{6}$ $\frac{1}{9}×7×13×\frac{9}{26}$

答案： $60×\frac{3}{2}×\frac{7}{9}$
$=90×\frac{7}{9}$
$=70$
$\frac{3}{4}×\frac{8}{7}×\frac{14}{15}$
$=\frac{6}{7}×\frac{14}{15}$
$=\frac{4}{5}$
$\frac{12}{5}×\frac{3}{8}×\frac{5}{6}$
$=\frac{9}{10}×\frac{5}{6}$
$=\frac{3}{4}$
$\frac{1}{9}×7×13×\frac{9}{26}$
$=(\frac{1}{9}×\frac{9}{26})×7×13$
$=\frac{1}{26}×7×13$
$=\frac{1}{26}×13×7$
$=\frac{1}{2}×7$
$=\frac{7}{2}$

3.(生活应用)望江县是全国油料生产大县,其油菜种植面积在安徽省各县中位居第一,油菜籽榨出来的油即为菜籽油。如图,倒出$\frac{2}{3}$瓶这样的菜籽油,倒出了多少升？每升菜籽油约$\frac{23}{25}$千克,一瓶菜籽油约多少千克？

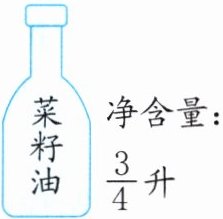
(图中为菜籽油瓶,净含量：$\frac{3}{4}$升)

答案： 解析：本题考查了分数乘法的应用。
第一问，已知一瓶菜籽油净含量为$\frac{3}{4}$升，倒出$\frac{2}{3}$瓶，用乘法计算：
$\frac{3}{4} × \frac{2}{3} = \frac{1}{2}（升）$。
第二问，已知每升菜籽油约$\frac{23}{25}$千克，一瓶菜籽油$\frac{3}{4}$升，用乘法计算：
$\frac{3}{4} × \frac{23}{25} = \frac{69}{100}（千克）$。
答案：$\frac{3}{4} × \frac{2}{3} = \frac{1}{2}（升）$，
$\frac{3}{4} × \frac{23}{25} = \frac{69}{100}（千克）$。
所以倒出了$\frac{1}{2}$升，一瓶菜籽油约$\frac{69}{100}$千克。

4.(科技民生)插秧机不仅适用于多种地形与种植模式,而且让农业生产更加高效。一台插秧机每小时插秧$\frac{3}{8}$公顷,6台这样的插秧机$\frac{4}{5}$小时可以插秧多少公顷？

答案： 解析：本题考查分数乘法的应用。
题干中给出了一台插秧机每小时插秧的公顷数，以及插秧机的台数和插秧的小时数，我们需要求出这些插秧机在给定时间内总共能插秧多少公顷。
首先，我们可以计算出一台插秧机在$\frac{4}{5}$小时内可以插秧多少公顷。这可以通过将一台插秧机每小时插秧的公顷数$\frac{3}{8}$与插秧的小时数$\frac{4}{5}$相乘来得出，
即$\frac{3}{8} × \frac{4}{5} = \frac{3}{10}$（公顷）。
接着，我们可以计算出6台插秧机在$\frac{4}{5}$小时内可以插秧多少公顷。这可以通过将一台插秧机在$\frac{4}{5}$小时内插秧的公顷数$\frac{3}{10}$与插秧机的台数6相乘来得出，
即$6 × \frac{3}{10} = \frac{9}{5} = 1.8$（公顷）。
或者我们可以先算出6台插秧机一小时插秧多少公顷，即$\frac{3}{8} × 6 = \frac{9}{4} $(公顷)，
然后再乘以时间$\frac{4}{5}$小时，即$\frac{9}{4} × \frac{4}{5} =\frac{9}{5} = 1.8$（公顷）。
答案：6台这样的插秧机$\frac{4}{5}$小时可以插秧1.8公顷。

5. 学校体育器材室里有80个篮球,足球的个数是篮球的$\frac{3}{4}$,排球的个数比足球少$\frac{1}{3}$。足球比排球多多少个？

答案： 解析：本题考查的知识点是分数乘法应用题的数量关系。解题的关键在于先根据已知条件求出足球的个数，再根据排球与足球个数的关系求出排球的个数，最后计算足球比排球多的个数。
答案：
足球的个数：$80×\frac{3}{4}=60$（个）
排球的个数：$60×(1 - \frac{1}{3}) = 60×\frac{2}{3}=40$（个）
足球比排球多的个数：$60 - 40 = 20$（个）
答：足球比排球多$20$个。

6.(算法探究)先找规律,再巧用规律解题。
$\frac{1}{2×3}= \frac{1}{2}-\frac{1}{3}$ $\frac{1}{3×4}= \frac{1}{3}-\frac{1}{4}$
$\frac{1}{4×5}= \frac{1}{4}-\frac{1}{5}$ $\frac{1}{5×6}= $( )$-$( )
$\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+…+\frac{1}{90}= $( )

答案： 解析：
本题考查的是分数的拆分与求和规律。
首先，观察给出的等式，可以发现一个规律：
对于形如$\frac{1}{n× (n+1)}$的分数，它可以拆分为$\frac{1}{n}-\frac{1}{n+1}$。
利用这个规律，可以将题目中的最后一项$\frac{1}{5× 6}$拆分为$\frac{1}{5}-\frac{1}{6}$。
接下来，看题目中的求和部分：
$\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\ldots+\frac{1}{90}$
这个求和可以看作是一系列形如$\frac{1}{n× (n+1)}$的分数的和。
根据之前的规律，可以将每个分数拆分为两部分，然后观察哪些部分可以相互抵消。
具体计算如下：
$\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\ldots+\frac{1}{90}$
$= \frac{1}{2× 3} + \frac{1}{3× 4} + \frac{1}{4× 5} + \ldots + \frac{1}{9× 10}$
$= (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + (\frac{1}{4} - \frac{1}{5}) + \ldots + (\frac{1}{9} - \frac{1}{10})$
观察上式，可以发现从第二项开始，每两项之间都有一部分可以相互抵消，最终只剩下第一项的$\frac{1}{2}$和最后一项的$-\frac{1}{10}$。
因此，求和结果为：
$\frac{1}{2} - \frac{1}{10} = \frac{5}{10} - \frac{1}{10} = \frac{4}{10} = \frac{2}{5}$
答案：$\frac{1}{5}$；$\frac{1}{6}$；$\frac{2}{5}$