1. (1)直线和圆有
(2)直线和圆
(3)直线和圆
两
个公共点,则这条直线和圆相交,这条直线叫做圆的割线
;(2)直线和圆
只有一
个公共点,则这条直线和圆相切,这条直线叫做圆的切线
;(3)直线和圆
没有
公共点,则这条直线和圆相离.
答案:
1.
(1)两 割线
(2)只有一 切线
(3)没有
(1)两 割线
(2)只有一 切线
(3)没有
2. 设$\odot O的半径为r$,圆心$O到直线l的距离为d$,则:(1)直线$l和\odot O相交\Leftrightarrow$
d<r
;(2)直线$l和\odot O相切\Leftrightarrow$d=r
;(3)直线$l和\odot O相离\Leftrightarrow$d>r
.
答案:
2.
(1)d<r
(2)d=r
(3)d>r
(1)d<r
(2)d=r
(3)d>r
1. 已知$\odot O的半径等于8\mathrm{~cm}$,圆心$O到直线l的距离为9\mathrm{~cm}$,则直线$l与\odot O$的公共点的个数为 (
A.0
B.1
C.2
D.无法确定
A
)A.0
B.1
C.2
D.无法确定
答案:
A
2. 如图,已知圆$O$的半径为 6,点$O$到某条直线的距离为 8,则这条直线可以是 (
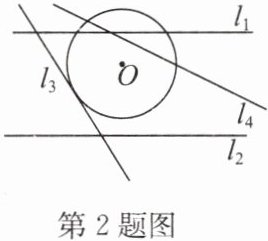
A.$l_{1}$
B.$l_{2}$
C.$l_{3}$
D.$l_{4}$
B
)
A.$l_{1}$
B.$l_{2}$
C.$l_{3}$
D.$l_{4}$
答案:
B
3. 在平面直角坐标系中,以点$A(2,1)$为圆心,1 为半径的圆与$x$轴的位置关系是 (
A.相离
B.相切
C.相交
D.不确定
B
)A.相离
B.相切
C.相交
D.不确定
答案:
B
4. $\mathrm{Rt}\triangle ABC$中,$\angle C= 90^{\circ}$,$AC= 6$,$AB= 10$,若以点$C$为圆心,$r为半径的圆与AB$所在的直线相交,则$r$可能为 (
A.3
B.4
C.4.8
D.5
D
)A.3
B.4
C.4.8
D.5
答案:
D
5. 已知圆$O的直径为13\mathrm{~cm}$,圆心$O到直线l_{1}$,$l_{2}$,$l_{3}的距离分别为4.5\mathrm{~cm}$,$6.5\mathrm{~cm}$,$8\mathrm{~cm}$,那么直线$l_{1}$,$l_{2}$,$l_{3}与圆O$分别是什么位置关系? 分别有几个公共点?
答案:
5.解:由圆O的直径为13cm,知半径为6.5cm.
∵圆心O到直线l₁的距离为4.5cm,小于半径,
∴直线l₁与圆O相交,有2个公共点
∵圆心O到直线l₂的距离为6.5cm,等于半径,
∴直线l₂与圆O相切,有1个公共点
∵圆心O到直线l₃的距离为8cm,大于半径,
∴直线l₃与圆O相离,没有公共点
∵圆心O到直线l₁的距离为4.5cm,小于半径,
∴直线l₁与圆O相交,有2个公共点
∵圆心O到直线l₂的距离为6.5cm,等于半径,
∴直线l₂与圆O相切,有1个公共点
∵圆心O到直线l₃的距离为8cm,大于半径,
∴直线l₃与圆O相离,没有公共点
6. 如图,在$\mathrm{Rt}\triangle ABC$中,$\angle C= 90^{\circ}$,$\angle B= 30^{\circ}$,$BC= 4\mathrm{~cm}$,以点$C$为圆心,$2\mathrm{~cm}$长为半径作圆,试判断$\odot C与直线AB$的位置关系.


答案:
6.解:如答图,作CD⊥AB于点D.
在Rt△BCD中,
∵∠B=30°,BC=4cm,
∴CD=1/2BC=2cm,
即圆心C到直线AB的距离CD等于圆的半径,
∴⊙C与直线AB相切.

6.解:如答图,作CD⊥AB于点D.
在Rt△BCD中,
∵∠B=30°,BC=4cm,
∴CD=1/2BC=2cm,
即圆心C到直线AB的距离CD等于圆的半径,
∴⊙C与直线AB相切.

查看更多完整答案,请扫码查看


