1. 利用
旋转的性质
可以求线段长、角的度数及图形的面积.
答案:
旋转的性质
2. 旋转作图的步骤:(1)找出图形的
特殊点
;(2)确定旋转中心
、旋转方向
和旋转角度
;(3)作出这些特殊点
的对应点;(4)按图形的顺序连接对应点
,得到旋转后的图形.
答案:
(1)特殊点
(2)中心 方向 角度
(3)这些特殊点
(4)对应点
(1)特殊点
(2)中心 方向 角度
(3)这些特殊点
(4)对应点
1. 如图,将$\triangle ABC绕点C按逆时针方向旋转75^{\circ}后得到\triangle A'B'C$,若$\angle ACB = 25^{\circ}$,则$\angle BCA'$的度数为 (
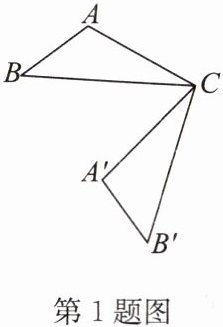
A.$50^{\circ}$
B.$40^{\circ}$
C.$25^{\circ}$
D.$60^{\circ}$
A
)
A.$50^{\circ}$
B.$40^{\circ}$
C.$25^{\circ}$
D.$60^{\circ}$
答案:
A
2. 如图,点$A,B,C,D,O$都在网格的格点上,若$\triangle COD是由\triangle AOB绕点O$按顺时针方向旋转得到的,则旋转的角度为 (
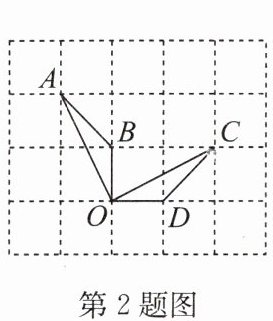
A.$60^{\circ}$
B.$135^{\circ}$
C.$45^{\circ}$
D.$90^{\circ}$
D
)
A.$60^{\circ}$
B.$135^{\circ}$
C.$45^{\circ}$
D.$90^{\circ}$
答案:
D
3. 如图,在$\triangle ABC$中$,AB = 2,BC = 3.6,\angle B = 60^{\circ},$将$\triangle ABC$绕点A顺时针旋转一定角度得到$\triangle ADE,$当点B的对应点D恰好落在BC边上时,则CD的长为
1.6
.
答案:
1.6
4. 如图,边长为$3的正方形ABCD绕点A逆时针旋转30^{\circ}得到正方形AB'C'D'$,则它们的公共部分的面积为
$3\sqrt{3}$
.
答案:
$3\sqrt{3}$
查看更多完整答案,请扫码查看


