5. 如图,在平面直角坐标系中,$\triangle ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3)$.
(1)$\triangle ABC$的面积是____;
(2)若$\triangle ABC经过平移后得到\triangle A_1B_1C_1$,已知点$C_1的坐标为(4,0)$,写出点$A_1$的坐标;
(3)将$\triangle ABC绕点O按顺时针方向旋转90^{\circ}得到\triangle A_2B_2C_2$,画出$\triangle A_2B_2C_2并写出点C_2$的坐标.
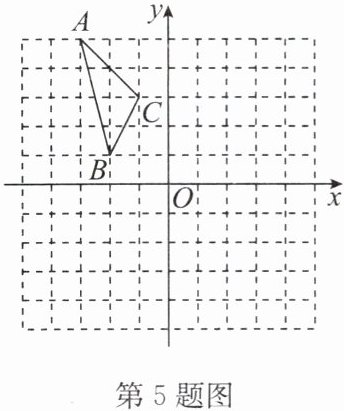
(1)$\triangle ABC$的面积是____;
(2)若$\triangle ABC经过平移后得到\triangle A_1B_1C_1$,已知点$C_1的坐标为(4,0)$,写出点$A_1$的坐标;
(3)将$\triangle ABC绕点O按顺时针方向旋转90^{\circ}得到\triangle A_2B_2C_2$,画出$\triangle A_2B_2C_2并写出点C_2$的坐标.

答案:
(1)3
(2)解:
∵△ABC经过平移后得到△A₁B₁C₁,点C₁的坐标为(4,0),
∴平移的方向和距离为向下平移3个单位长度,向右平移5个单位长度,
∴点A₁的坐标为(2,2).
(3)解:如答图,△A₂B₂C₂即为所求,点C₂的坐标为(3,1).

(1)3
(2)解:
∵△ABC经过平移后得到△A₁B₁C₁,点C₁的坐标为(4,0),
∴平移的方向和距离为向下平移3个单位长度,向右平移5个单位长度,
∴点A₁的坐标为(2,2).
(3)解:如答图,△A₂B₂C₂即为所求,点C₂的坐标为(3,1).

1. 把一个图形绕着某一点旋转
180°
,如果它能够与另一个图形重合
,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心
(简称中心)。这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点。
答案:
180° 另一个图形重合 对称中心
2. 中心对称的性质:中心对称的两个图形,对称点所连线段都
经过对称中心
,而且被对称中心所平分
;中心对称的两个图形是全等图形
。
答案:
经过对称中心 被对称中心所平分 全等图形
1. 下列图形中,$\triangle A^{\prime} B^{\prime} C^{\prime}与\triangle ABC$成中心对称的是(

A
) 
答案:
A
查看更多完整答案,请扫码查看


