1. 如果一个多边形的
所有顶点
都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
答案:
所有顶点
2. 圆内接四边形的对角
互补
.
答案:
互补
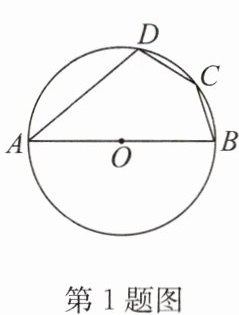
1. 如图,四边形 ABCD 内接于$\odot O$,若$∠A= 40^{\circ }$,则$∠C= $ (
A.$110^{\circ }$
B.$120^{\circ }$
C.$135^{\circ }$
D.$140^{\circ }$
D
)
A.$110^{\circ }$
B.$120^{\circ }$
C.$135^{\circ }$
D.$140^{\circ }$
答案:
D
2. 如图,在$\odot O$的内接四边形 ABCD 中,$∠BOD= 120^{\circ }$,那么$∠BCD$的度数是 (
A.$120^{\circ }$
B.$100^{\circ }$
C.$80^{\circ }$
D.$60^{\circ }$
A
)A.$120^{\circ }$
B.$100^{\circ }$
C.$80^{\circ }$
D.$60^{\circ }$
答案:
A
3. 如图,四边形 ABCD 为$\odot O$的内接四边形,$∠A= 100^{\circ }$,则$∠DCE$的度数为
100°
.
答案:
100°
4. 在圆内接四边形 ABCD 中,若$∠A,∠B,∠C的度数之比为4:3:5$,则$∠D$的度数是
120°
.
答案:
120°
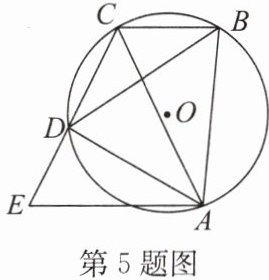
5. 如图,四边形 ABCD 内接于$\odot O$,AC 与 BD 为对角线,$∠BCA= ∠BAD$,过点 A 作$AE// BC$交 CD 的延长线于点 E.求证:$EC= AC.$

答案:
证明:
∵AE//BC,
∴∠E+∠ECB=180°,∠BCA=∠CAE.
∵四边形ABCD内接于⊙O,
∴∠BAD+∠ECB=180°,
∴∠E=∠BAD.
∵∠BCA=∠BAD,
∴∠E=∠CAE,
∴EC=AC.
∵AE//BC,
∴∠E+∠ECB=180°,∠BCA=∠CAE.
∵四边形ABCD内接于⊙O,
∴∠BAD+∠ECB=180°,
∴∠E=∠BAD.
∵∠BCA=∠BAD,
∴∠E=∠CAE,
∴EC=AC.
查看更多完整答案,请扫码查看


