3. 在函数① $ y = 4x^{2} $,② $ y = \frac{2}{3}x^{2} $,③ $ y = -\frac{4}{3}x^{2} $ 中,图象开口大小顺序用序号表示应为 (
A.① > ② > ③
B.① > ③ > ②
C.② > ③ > ①
D.② > ① > ③
C
)A.① > ② > ③
B.① > ③ > ②
C.② > ③ > ①
D.② > ① > ③
答案:
C
4. 已知 $ M(x_{1}, y_{1}) $,$ N(x_{2}, y_{2}) $ 是二次函数 $ y = 2x^{2} $ 的图象上两点,若 $ x_{1} < x_{2} < 0 $,则下列不等式一定成立的是 (
A.$ y_{1} \leq y_{2} $
B.$ y_{1} \geq y_{2} $
C.$ y_{1} < y_{2} $
D.$ y_{1} > y_{2} $
D
)A.$ y_{1} \leq y_{2} $
B.$ y_{1} \geq y_{2} $
C.$ y_{1} < y_{2} $
D.$ y_{1} > y_{2} $
答案:
D
5. 抛物线 $ y = \frac{1}{2}x^{2} $ 的开口向
上
,对称轴是y轴
,顶点坐标是(0,0)
。
答案:
上 y轴 (0,0)
6. 如果抛物线 $ y = (m - 1)x^{2} $ 的开口向上,那么 $ m $ 的取值范围是
m>1
。
答案:
m>1
7. 在如图所示的平面直角坐标系中,画出函数 $ y = 2x^{2} $,$ y = \frac{1}{2}x^{2} $,$ y = -2x^{2} $ 与 $ y = -\frac{1}{2}x^{2} $ 的图象。
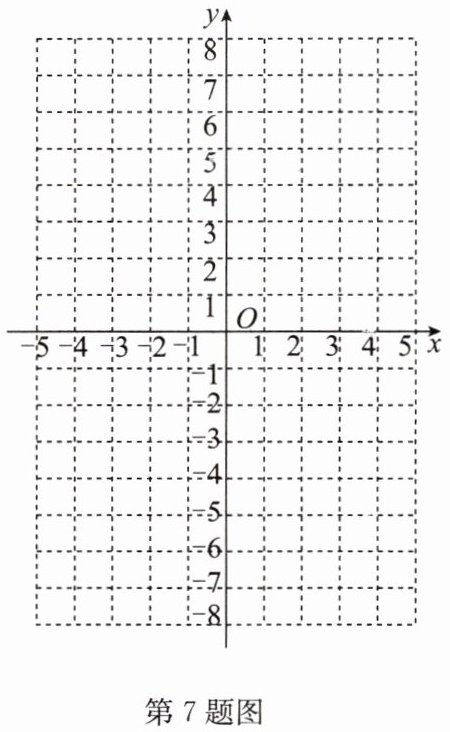

答案:
解:列表如下.
x -2 -1 0 1 2
y=2x² 8 2 0 2 8
y=1/2x² 2 1/2 0 1/2 2
y=-2x² -8 -2 0 -2 -8
y=-1/2x² -2 -1/2 0 -1/2 -2
描点:以表中的数据作为点的坐标在平面直角坐标系中描点.
连线:用平滑的线连接各点,如答图所示.

解:列表如下.
x -2 -1 0 1 2
y=2x² 8 2 0 2 8
y=1/2x² 2 1/2 0 1/2 2
y=-2x² -8 -2 0 -2 -8
y=-1/2x² -2 -1/2 0 -1/2 -2
描点:以表中的数据作为点的坐标在平面直角坐标系中描点.
连线:用平滑的线连接各点,如答图所示.

查看更多完整答案,请扫码查看


