2. 如图,$\triangle ABC与\triangle A^{\prime} B^{\prime} C^{\prime}关于点O$成中心对称,则下列结论不成立的是(
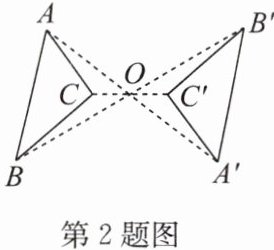
A.点$A与点A^{\prime}$是对称点
B.$B O= B^{\prime} O$
C.$A B / / A^{\prime} B^{\prime}$
D.$\angle A C B= \angle C^{\prime} A^{\prime} B^{\prime}$
D
)
A.点$A与点A^{\prime}$是对称点
B.$B O= B^{\prime} O$
C.$A B / / A^{\prime} B^{\prime}$
D.$\angle A C B= \angle C^{\prime} A^{\prime} B^{\prime}$
答案:
D
3. 如图,$\triangle A^{\prime} B^{\prime} C^{\prime}与\triangle ABC关于点O$成中心对称,$A B= B C= 2$,$\angle A B C= 120^{\circ}$,则$\angle B^{\prime} A^{\prime} C^{\prime}$的度数为
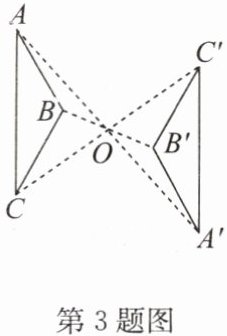
30°
。
答案:
30°
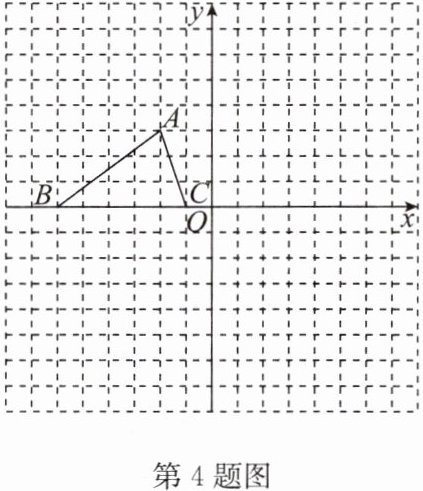
4. 如图,$\triangle ABC的三个顶点的坐标分别为A(-2,3)$,$B(-6,0)$,$C(-1,0)$。
(1)画出与$\triangle ABC关于点O成中心对称的图形\triangle A_{1} B_{1} C_{1}$;
(2)将$\triangle ABC绕坐标原点O按逆时针方向旋转90^{\circ}$,得到$\triangle A_{2} B_{2} C_{2}$,画出图形,并直接写出点$A_{2}$,$B_{2}$,$C_{2}$的坐标。
(1)画出与$\triangle ABC关于点O成中心对称的图形\triangle A_{1} B_{1} C_{1}$;
(2)将$\triangle ABC绕坐标原点O按逆时针方向旋转90^{\circ}$,得到$\triangle A_{2} B_{2} C_{2}$,画出图形,并直接写出点$A_{2}$,$B_{2}$,$C_{2}$的坐标。

答案:
4.解:
(1)如答图,△A₁B₁C₁即为所求.
(2)如答图,△A₂B₂C₂即为所求,点A₂,B₂,C₂的坐标分别为(-3,-2),(0,-6),(0,-1).

4.解:
(1)如答图,△A₁B₁C₁即为所求.
(2)如答图,△A₂B₂C₂即为所求,点A₂,B₂,C₂的坐标分别为(-3,-2),(0,-6),(0,-1).

1. 把一个图形
绕着某一个点旋转180°
,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
。
答案:
绕着某一个点旋转180° 对称中心
查看更多完整答案,请扫码查看


