1. 圆是轴对称图形,
任何一条直径所在直线
都是圆的对称轴.
答案:
任何一条直径所在直线
2. 垂直于弦的直径
平分弦
,并且平分弦所对的两条弧
.
答案:
平分弦 平分弦所对的两条弧
3. 平分弦(
不是直径
)的直径垂直于弦
,并且平分弦所对的两条弧
.
答案:
不是直径 垂直于弦 平分弦所对的两条弧
1. 在$\odot O$中,已知半径为 5,弦 AB 的长为 8,则圆心 O 到 AB 的距离为(
A.3
B.4
C.5
D.6
A
)A.3
B.4
C.5
D.6
答案:
A
2. 若$\odot O$的弦 AB 的长为 8 cm,弦 AB 的弦心距为 3 cm,则$\odot O$的半径为(
A.4 cm
B.5 cm
C.8 cm
D.10 cm
B
)A.4 cm
B.5 cm
C.8 cm
D.10 cm
答案:
B
3. 下列说法中正确的是(
A.垂直于弦的直线平分弦所对的两条弧
B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径
D.弦的垂直平分线经过圆心
D
)A.垂直于弦的直线平分弦所对的两条弧
B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径
D.弦的垂直平分线经过圆心
答案:
D
4. 如图,$\odot O的弦AB = 6$,M 是 AB 上任意一点,且 OM 的最小值为 4,则$\odot O$的半径为(
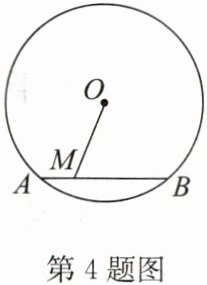
A.2
B.3
C.4
D.5
D
)
A.2
B.3
C.4
D.5
答案:
D
5. 如图,已知 MN 是$\odot O$的直径,AB 是$\odot O$的弦,$AB\perp MN$,点 C 在线段 AB 上,$OC = AC = 2$,$BC = 4$,求$\odot O$的半径.
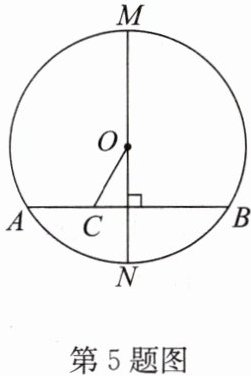

答案:
解:连接OB,设AB与MN交于点D,如答图.
∵AC=2,BC=4,
∴AB=AC+BC=6.
∵AB⊥MN,
∴AD=BD=$\frac{1}{2}$AB=3,
∠ODC=∠ODB=90°,
∴CD=AD−AC=1,
∴OD=$\sqrt{OC^2-CD^2}$=$\sqrt{2^2-1^2}$=$\sqrt{3}$,
∴OB=$\sqrt{OD^2+BD^2}$=$\sqrt{(\sqrt{3})^2+3^2}$=2$\sqrt{3}$
即⊙O的半径为2$\sqrt{3}$

解:连接OB,设AB与MN交于点D,如答图.
∵AC=2,BC=4,
∴AB=AC+BC=6.
∵AB⊥MN,
∴AD=BD=$\frac{1}{2}$AB=3,
∠ODC=∠ODB=90°,
∴CD=AD−AC=1,
∴OD=$\sqrt{OC^2-CD^2}$=$\sqrt{2^2-1^2}$=$\sqrt{3}$,
∴OB=$\sqrt{OD^2+BD^2}$=$\sqrt{(\sqrt{3})^2+3^2}$=2$\sqrt{3}$
即⊙O的半径为2$\sqrt{3}$

查看更多完整答案,请扫码查看


