《2025年名校课堂七年级数学上册人教版山西专版》

9. (2024·忻州期末)粽子作为中国历史文化积淀最深厚的传统食品之一,传播甚远.某家庭制作的粽子礼盒每份由6个蛋黄肉粽和4个碱水粽组成.用1千克糯米可制作24个蛋黄肉粽或16个碱水粽,现要用6千克糯米制作粽子,则用3千克糯米制作蛋黄肉粽,余下的糯米制作碱水粽,才能恰好使制作的蛋黄肉粽和碱水粽配套.

答案： 9.3

10. (教材P133例2变式)整理一批图书,若由一个人单独做需要80小时完成,假设每个人的工作效率相同.若限定32小时完成,由一个人先做8小时,则至少需要再增加多少人帮忙,才能在规定的时间内完成?

答案： 10.解：设再增加x人帮忙，恰好在规定的时间内完成.根据题意，得$\frac{8}{80}$+$\frac{32-8}{80}$(x+1)=1，解得x=2.答：至少需要再增加2人帮忙，才能在规定的时间内完成.

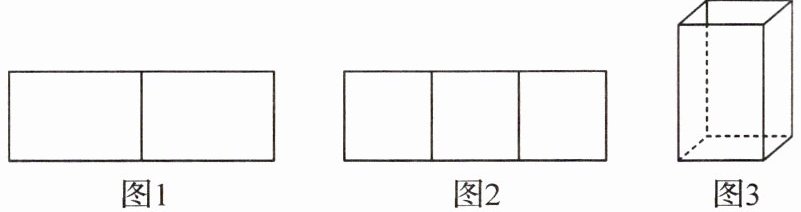
11. 杭州外国语校本经典题 如图,将某种规格的长方形纸板按照如图1、图2所示的两种方法裁剪,分别可裁得2块相同的小长方形纸板和3块相同的小正方形纸板.已知4块小长方形纸板和1块小正方形纸板可做成如图3所示的无盖长方体纸盒.如果这种规格的长方形纸板共有21张,那么怎样裁剪这些纸板,可使做成的无盖纸盒数最多?最多能做多少个?

答案： 11.解：设用x张裁剪成小长方形纸板，则用(21-x)张裁剪成小正方形纸板.根据题意，得$\frac{2x}{4}$=$\frac{3(21-x)}{1}$，解得x=18.
∴21-x=21-18=3，$\frac{2x}{4}$=$\frac{2×18}{4}$=9.答：用18张裁剪成小长方形纸板，3张裁剪成小正方形纸板，可使做成的无盖纸盒数最多，最多能做9个.

12. (2024·吕梁孝义市期末)阅读下列材料,完成相应任务.
数学课堂上,李老师出示了如下信息:
信息一:某服装厂计划用4032m布料加工成学生校服,已知每3m布料可以加工成2件上衣或3条裤子,且2件上衣和1条裤子配成1套校服.
信息二:一人整理这批校服需要40h完成,现计划由一部分人先整理4h,然后增加2人与他们一起再整理8h,完成这项工作(假设这些人的工作效率相同).
任务一:根据信息一,李老师提出问题:应如何安排布料加工,才能使上衣和裤子刚好配套?能加工成多少套校服?
小颖和小彬分别列出了尚不完整的方程如下:
小颖列的方程是$\frac{3}{2}×2x+$? $=4032$;
小彬列的方程是$\frac{x}{?}=\frac{2(4032-x)}{\frac{3}{3}}$.
①小颖同学所列方程中,x表示加工的校服套数,“?”处应填$\frac{3}{3}x$.
②小彬同学所列方程中,x表示加工成上衣的布料长度,$\frac{2(4032-x)}{\frac{3}{3}}$表示加工的裤子数量的2倍.
任务二:小亮根据信息二提出了问题:应安排多少人先整理4h?请解决这个问题,并写出解答过程.

答案： 12.解：任务一：①加工的校服套数 $\frac{3}{3}x$ ②加工成上衣的布料长度 加工的裤子数量的2倍 任务二：设应安排y人先整理4h，将整理这批校服的工作总量看作“1”，则每个人的工作效率为$\frac{1}{40}$.由题意，得$\frac{4y}{40}$+$\frac{8(y+2)}{40}$=1，解得y=2.答：应安排2人先整理4h.