第106页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. (2024·太原三十七中月考)已知下列方程:
①$\frac{x}{3}+8=3$;②$18-x$;③$1=2x+2$;④$5x^{2}=20$;⑤$x+y=8$。其中是一元一次方程的有(
A.1 个
B.2 个
C.3 个
D.4 个
①$\frac{x}{3}+8=3$;②$18-x$;③$1=2x+2$;④$5x^{2}=20$;⑤$x+y=8$。其中是一元一次方程的有(
B
)A.1 个
B.2 个
C.3 个
D.4 个
答案:
1.B
2. (2024·忻州五台县期末联考)已知$x=-2$是关于$x$的一元一次方程$mx-2=0$的解,则$m$的值为(
A.-1
B.0
C.1
D.2
A
)A.-1
B.0
C.1
D.2
答案:
2.A
3. 新考向 开放性问题 请写出一个满足下列条件的一元一次方程:①未知数$x$的系数为负数;②方程左边只有两项,并含有数字 5;③方程的解为$x=1$。则这个方程可以是
-x+5=4(答案不唯一)
。
答案:
3.-x+5=4(答案不唯一)
4. (2024·大同云州区期末)若$3a-2b=5$,则下列等式中不一定成立的是(
A.$3a-5=2b$
B.$3a+1=2b+6$
C.$3ac=2bc+5$
D.$a=\frac{2}{3}b+\frac{5}{3}$
C
)A.$3a-5=2b$
B.$3a+1=2b+6$
C.$3ac=2bc+5$
D.$a=\frac{2}{3}b+\frac{5}{3}$
答案:
4.C
5. 张萌的手中有若干个相同大小的铁球、正方体和圆柱,她将它们放在天平上,使天平保持平衡,如图所示,则 3 个铁球的质量等于
 ]
]
9
个正方体的质量。 ]
]
答案:
5.9
6. (2024·吕梁交城县期末)阿拉伯数学家花拉子米著有《代数学》(又称《还原与对消计算概要》),推动了古代数学的进步,为人类解方程问题提供了简便的方法。我国古代数学著作《九章算术》的“方程”章,更早使用了“对消”和“还原”的方法。“对消”和“还原”具体指的是解方程中的(
A.去分母、移项
B.去括号、合并同类项
C.去分母、合并同类项
D.合并同类项、移项
D
)A.去分母、移项
B.去括号、合并同类项
C.去分母、合并同类项
D.合并同类项、移项
答案:
6.D
7. (2023·吕梁离石区期末)已知方程$\frac{3x-1}{2}-1=-\frac{x+2}{6}$,去分母后正确的结果是(
A.$3(3x-1)-1=-x+2$
B.$3(3x-1)-1=-(x+2)$
C.$3(3x-1)-6=-x+2$
D.$3(3x-1)-6=-(x+2)$
D
)A.$3(3x-1)-1=-x+2$
B.$3(3x-1)-1=-(x+2)$
C.$3(3x-1)-6=-x+2$
D.$3(3x-1)-6=-(x+2)$
答案:
7.D
8. 解方程:
(1)$4-(x+3)=2(x-1)$。
(2)$\frac{0.1x+0.3}{0.2}+2.5=\frac{0.4x-1}{0.5}$。
(1)$4-(x+3)=2(x-1)$。
(2)$\frac{0.1x+0.3}{0.2}+2.5=\frac{0.4x-1}{0.5}$。
答案:
8.解:
(1)去括号,得4-x-3=2x-2.移项,得-x-2x=-2+3-4.合并同类项,得-3x=-3.系数化为1,得x=1.
(2)去分母,得5(x+3)+25=2(4x-10).去括号,得5x+15+25=8x-20.移项,得5x-8x=-20-25-15.合并同类项,得-3x=-60.系数化为1,得x=20.
(1)去括号,得4-x-3=2x-2.移项,得-x-2x=-2+3-4.合并同类项,得-3x=-3.系数化为1,得x=1.
(2)去分母,得5(x+3)+25=2(4x-10).去括号,得5x+15+25=8x-20.移项,得5x-8x=-20-25-15.合并同类项,得-3x=-60.系数化为1,得x=20.
9. (2024·忻州忻府区期末)“一针绘梦乡,一线织华装。”中国传统手工艺在新的时代里正绽放出更加绚丽的光彩。我市某传统手工坊计划做一批折扇,如果每人做 7 把,那么将比计划的多做 9 把;如果每人做 5 把,那么将比计划的少做 5 把。设计划做$x$把折扇,则可列方程为(
A.$\frac{x-9}{7}=\frac{x+5}{5}$
B.$7x-9=5x+5$
C.$\frac{x+9}{7}=\frac{x-5}{5}$
D.$7x+9=5x-5$
C
)A.$\frac{x-9}{7}=\frac{x+5}{5}$
B.$7x-9=5x+5$
C.$\frac{x+9}{7}=\frac{x-5}{5}$
D.$7x+9=5x-5$
答案:
9.C
10. (2024·朔州期末联考)强强利用两个完全相同的瓶子和一些沙子做成了如图所示的沙漏(两瓶子的瓶底相连,中间有一个小孔)。初始时刻上方瓶子中沙子的高度为 17 cm,终止时刻下方的瓶子中空余部分的高度为 3 cm。若每个瓶子的容积都为 2000 cm³,则沙子的体积为(
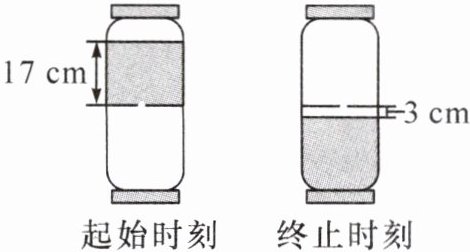
A.300 cm³
B.1700 cm³
C.2000 cm³
D.2300 cm³
]
B
)
A.300 cm³
B.1700 cm³
C.2000 cm³
D.2300 cm³
]
答案:
10.B
查看更多完整答案,请扫码查看


