《2025年暑假乐园八年级理科版辽宁师范大学出版社》

11. 如图，在四边形$ABDC$中，$\angle D = \angle B = 90^{\circ}$，点$O$为$BD$的中点，且$OA$平分$\angle BAC$.
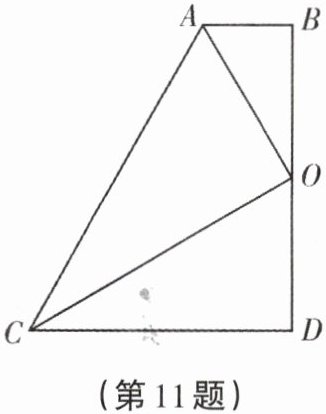
(1) 求证：$CO$平分$\angle ACD$.
证明：过点 $O$ 作 $OE\perp AC$ 于点 $E$。$\because\angle B=90^{\circ}$，$OA$ 平分 $\angle BAC$，$\therefore OB=OE$。$\because$ 点 $O$ 为 $BD$ 的中点，$\therefore OB=OD$。$\therefore OE=OD$。$\therefore CO$ 平分 $\angle ACD$。
(2) 求证：$OA \perp OC$.
证明：在 $Rt\triangle ABO$ 和 $Rt\triangle AEO$ 中，$AO=AO$，$OB=OE$，$\therefore Rt\triangle ABO\cong Rt\triangle AEO(HL)$。$\therefore\angle AOB=\angle AOE$。同理可得 $\angle COD=\angle COE$。$\therefore\angle AOC=\angle AOE+\angle COE=\frac{1}{2}\angle BOE+\frac{1}{2}\angle DOE=90^{\circ}$，即 $OA\perp OC$。
(3) 求证：$AB + CD = AC$.
证明：由(2)知，$Rt\triangle ABO\cong Rt\triangle AEO$，$\therefore AB=AE$。同理可得 $CD=CE$。$\because AC=AE+CE$，$\therefore AB+CD=AC$。

答案： 证明：
(1)过点 $O$ 作 $OE\perp AC$ 于点 $E$。$\because\angle B=90^{\circ}$，$OA$ 平分 $\angle BAC$，$\therefore OB=OE$。$\because$ 点 $O$ 为 $BD$ 的中点，$\therefore OB=OD$。$\therefore OE=OD$。$\therefore CO$ 平分 $\angle ACD$。
(2)在 $Rt\triangle ABO$ 和 $Rt\triangle AEO$ 中，$AO=AO$，$OB=OE$，$\therefore Rt\triangle ABO\cong Rt\triangle AEO(HL)$。$\therefore\angle AOB=\angle AOE$。同理可得 $\angle COD=\angle COE$。$\therefore\angle AOC=\angle AOE+\angle COE=\frac{1}{2}\angle BOE+\frac{1}{2}\angle DOE=90^{\circ}$，即 $OA\perp OC$。
(3)由
(2)知，$Rt\triangle ABO\cong Rt\triangle AEO$，$\therefore AB=AE$。同理可得 $CD=CE$。$\because AC=AE+CE$，$\therefore AB+CD=AC$。

12. 已知点$O$是线段$AB$的中点，点$P$是直线$l$上的任意一点，分别过点$A$和点$B$作直线$l$的垂线，垂足分别为点$C$和点$D$. 我们定义垂足与中点之间的距离为“足中距”.
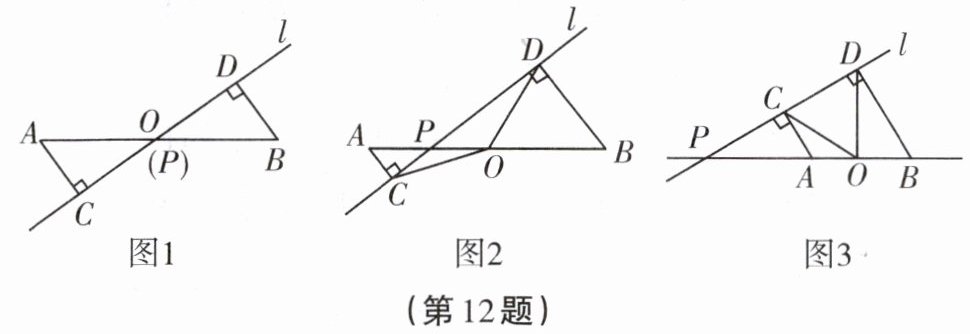
(1)【猜想验证】如图$1$，当点$P$与点$O$重合时，请你猜想、验证后直接写出“足中距”$QC$和$OD$的数量关系：______.
(2)【探究证明】如图$2$，当点$P$是线段$AB$上任意一点时，(1)中的“足中距”$OC$和$OD$的数量关系是否依然成立？若成立，请给出证明；若不成立，请说明理由.
(3)【拓展延伸】如图$3$，①当点$P$是线段$BA$延长线上任意一点时，(1)中的“足中距”$OC$和$OD$的数量关系是否依然成立？若成立，请给出证明；若不成立，请说明理由.
②若$\angle COD = 60^{\circ}$，请直接写出线段$AC$，$BD$，$OC$之间的数量关系.

答案：

(1) $OC=OD$
(2)解：$OC=OD$ 依然成立。证明如下：如图 1，过点 $O$ 作直线 $EF// CD$，交 $AC$ 的延长线于点 $E$，交 $BD$ 于点 $F$。$\because AC\perp CD$，$BD\perp CD$，$\therefore\angle ACD=\angle BDC=90^{\circ}$，$\therefore AE// DF$。$\therefore$ 四边形 $CEFD$ 是平行四边形。$\therefore\angle BDC=\angle CEF=90^{\circ}$，$CE=DF$。由
(1)知 $OE=OF$，又 $\because\angle CEO=\angle DFO$，$\therefore\triangle COE\cong\triangle DOF(SAS)$。$\therefore OC=OD$。

(3)①解：$OC=OD$ 依然成立。证明如下：如图 2，分别延长 $CO$，$DB$ 交于点 $E$。$\because AC\perp CD$，$BD\perp CD$，$\therefore\angle ACP=\angle BDP=90^{\circ}$，$\therefore AC// BD$，$\therefore\angle ACO=\angle E$。$\because$ 点 $O$ 为 $AB$ 的中点，$\therefore AO=BO$。又 $\because\angle AOC=\angle BOE$，$\therefore\triangle AOC\cong\triangle BOE(AAS)$。$\therefore OC=OE$。$\because\angle CDE=90^{\circ}$，$\therefore OD=OC$。② $AC+BD=\sqrt{3}OC$。