《2025年君杰文化假期课堂暑假作业八年级数学沪科版》

7. 如图,四边形$ABCD$是平行四边形,$BE$,$DF分别是\angle ABC$,$\angle ADC$的平分线,且与对角线$AC分别相交于点E$,$F$。求证：$AE = CF$。

答案： 【解析】：根据平行四边形的性质，对边平行，对角相等，证明$\triangle ABE$和$\triangle CDF$全等，利用全等三角形的性质即可得出$AE = CF$。
证明：
∵四边形$ABCD$是平行四边形，
∴$AB = CD$，$\angle ABC = \angle ADC$，$AB// CD$，
∴$\angle BAE = \angle DCF$，
∵$BE$，$DF$分别是$\angle ABC$，$\angle ADC$的平分线，
∴$\angle ABE = \frac{1}{2}\angle ABC$，$\angle CDF = \frac{1}{2}\angle ADC$，
∴$\angle ABE = \angle CDF$，
在$\triangle ABE$和$\triangle CDF$中，
$\begin{cases} \angle BAE = \angle DCF, \\ AB = CD, \\ \angle ABE = \angle CDF. \end{cases}$
∴$\triangle ABE \cong \triangle CDF(ASA)$，
∴$AE = CF$。
【答案】：证明：
∵四边形$ABCD$是平行四边形，
∴$AB = CD$，$\angle ABC = \angle ADC$，$AB// CD$，
∴$\angle BAE = \angle DCF$，
∵$BE$，$DF$分别是$\angle ABC$，$\angle ADC$的平分线，
∴$\angle ABE = \frac{1}{2}\angle ABC$，$\angle CDF = \frac{1}{2}\angle ADC$，
∴$\angle ABE = \angle CDF$，
在$\triangle ABE$和$\triangle CDF$中，
$\begin{cases} \angle BAE = \angle DCF, \\ AB = CD, \\ \angle ABE = \angle CDF. \end{cases}$
∴$\triangle ABE \cong \triangle CDF(ASA)$，
∴$AE = CF$。

8. 如图,在$□ ABCD$中,$AC交BD于点O$,点$E$,点$F分别是OA$,$OC$的中点,请判断线段$BE$,$DF$的关系,并证明你的结论。

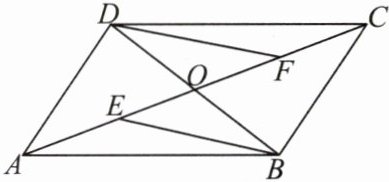
答案： $BE=DF$，$BE// DF$（提示：连接 DE，BF，证明四边形 BEDF 为平行四边形）

9. 如图,已知四边形$ABCD的对角线AC与BD相交于点O$,且$AC = BD$,$M$,$N分别是AB$,$CD$的中点,$MN分别交BD$,$AC于点E$,$F$。你能说出$OE与OF$的大小关系并加以证明吗？

答案： $OE=OF$（提示：取 AD 中点 G，连 MG，NG）