《2025年快乐过暑假江苏凤凰科学技术出版社八年级提优版》

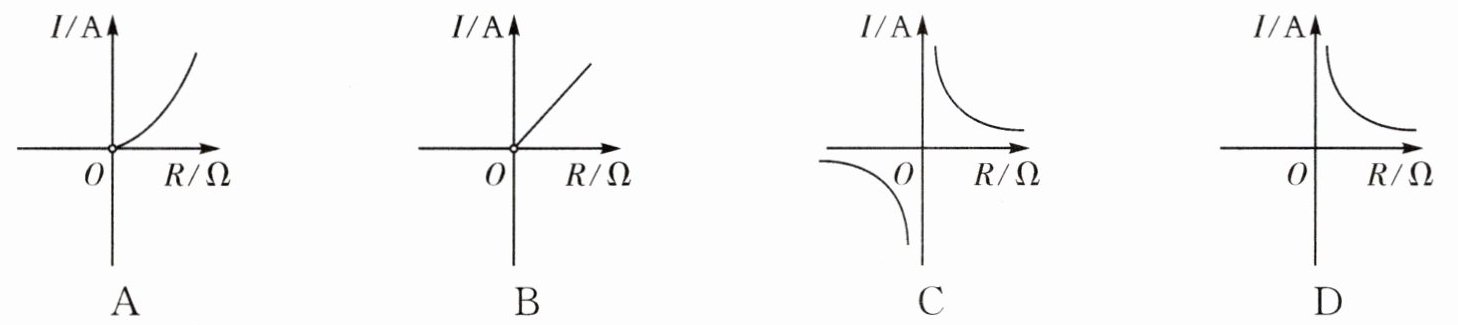
1. 已知蓄电池的电压 $ U $ 为定值,使用蓄电池时,电流 $ I $(单位: $ \mathrm{A} $)与电阻 $ R $(单位: $ \Omega $)是反比例函数关系$ \left(I= \frac{U}{R}\right) $.下列反映电流 $ I $ 与电阻 $ R $ 之间函数关系的图像大致是(C).

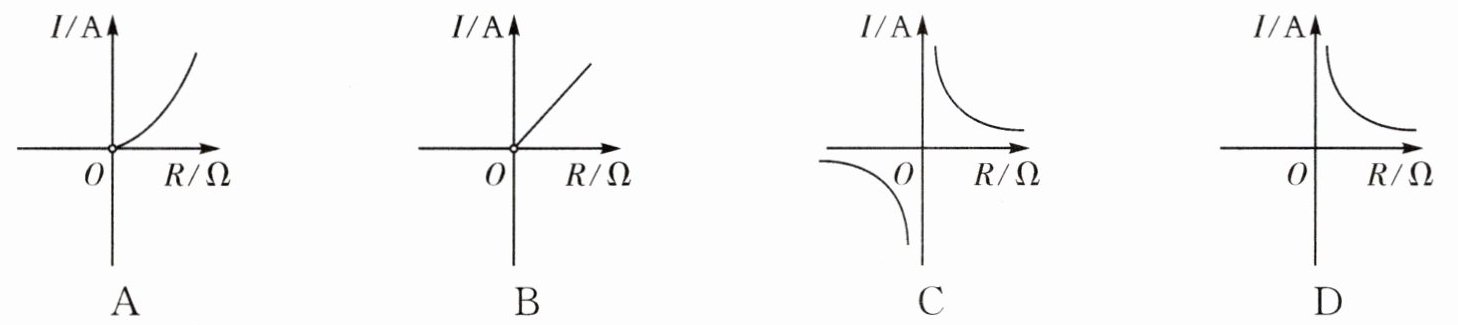
答案： C

2. 某杠杆装置如图,杆的一端吊起一桶水,阻力臂保持不变,在使杠杆平衡的情况下,小明通过改变动力臂 $ l $,测量出相应的动力 $ F $ 数据如表:(动力 $ × $ 动力臂 $ = $ 阻力 $ × $ 阻力臂)

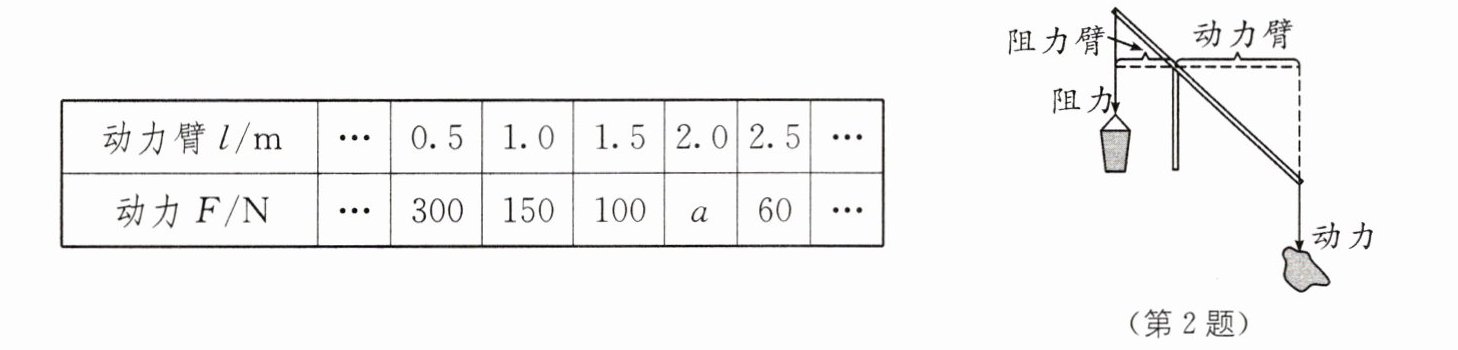
请根据表中数据规律探求,当动力臂长度为 $ 2.0 \mathrm{~m} $ 时,所需动力是(B).
A.$ 150 \mathrm{~N} $
B.$ 90 \mathrm{~N} $
C.$ 75 \mathrm{~N} $
D.$ 60 \mathrm{~N} $

答案： B

3. 机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度 $ v(\mathrm{~m} / \mathrm{s}) $ 是载重后总质量 $ m(\mathrm{~kg}) $ 的反比例函数.已知一款机器狗载重后总质量 $ m= 60 \mathrm{~kg} $ 时,它的最快移动速度 $ v= 6 \mathrm{~m} / \mathrm{s} $;当其载重后总质量 $ m= 90 \mathrm{~kg} $ 时,它的最快移动速度 $ v= $______4$ \mathrm{m} / \mathrm{s} $.

答案： 1. 首先设反比例函数关系式：
因为$v$是$m$的反比例函数，所以设$v = \frac{k}{m}(k\neq0)$。
2. 然后求$k$的值：
已知当$m = 60\mathrm{kg}$时，$v = 6\mathrm{m/s}$，把$m = 60$，$v = 6$代入$v=\frac{k}{m}$中，可得$6=\frac{k}{60}$。
根据等式的性质，两边同时乘以$60$，解得$k = 6×60=360$。
所以反比例函数关系式为$v=\frac{360}{m}$。
3. 最后求当$m = 90\mathrm{kg}$时$v$的值：
当$m = 90$时，把$m = 90$代入$v=\frac{360}{m}$中，得$v=\frac{360}{90}$。
计算$\frac{360}{90}=4$。
故答案为$4$。

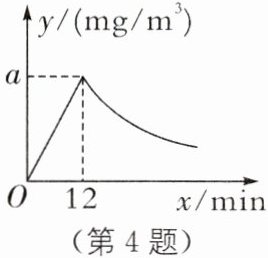
4. 如图,某药剂在空气中的浓度 $ y\left(\mathrm{mg} / \mathrm{m}^3\right) $ 与时间 $ x(\mathrm{~min}) $ 之间先满足正比例函数的关系,再满足反比例函数的关系,且当 $ x= 12 $ 时, $ y $ 有最大值,最大值为 $ a $,则当 $ y= \frac{2}{3} a $ 时, $ x $ 的值是______$-2a$.

答案： $-2a$

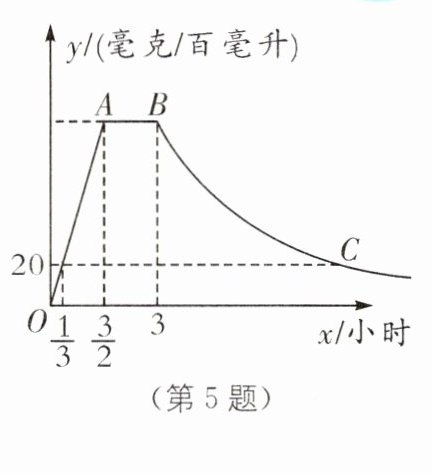
5. 某生物小组探究“酒精对人体的影响”,资料显示,一般饮用低度白酒 $ 100 $ 毫升后,血液中酒精含量 $ y $(毫克/百毫升)与时间 $ x $(小时)的关系可近似地用如图所示的图像表示.国家规定,人体血液中的酒精含量大于或等于 $ 20 $(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求图中线段 $ O A $ 所在直线的函数表达式.
(2)当 $ x \geqslant 3 $ 时, $ y $ 与 $ x $ 成反比例关系.假设某人晚上 $ 19: 00 $ 喝完 $ 100 $ 毫升低度白酒,那么此人第二天早上 $ 9: 00 $ 能否驾车出行? 请说明理由.

答案： 5. $\sqrt{2}$（答案不唯一）