2025年暑假衔接起跑线小升初数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接起跑线小升初数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 一个长方形的周长是 32 cm,长和宽的比是 $ 5:3 $,这个长方形的面积是(
60
) $ cm^{2} $。
答案:
60
2. 如图,把一个圆剪拼成一个近似的长方形,已知长方形的周长是 33.12 cm,则阴影部分的面积是(
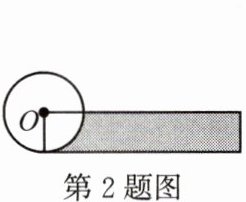
$12\pi$
) $ cm^{2} $。
答案:
$12\pi$
3. 一个长 5 cm,宽 2.4 cm 的长方形,沿对角线对折后,得到如图所示的几何图形,阴影部分的周长是(
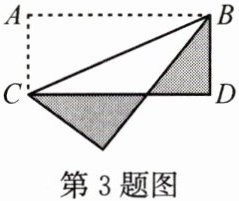
14.8
)cm。
答案:
14.8
4. 一个长方形的宽是长的 $ \frac{3}{5} $,如果宽增加了 10 cm,则长方形变成正方形,原来长方形的周长是(
80
)cm,面积是(375
) $ cm^{2} $。
答案:
80 375
5. 把一个圆形纸片沿半径剪开,等分后再拼成一个宽等于半径、面积相等的近似长方形,已知圆形面积为 $ 12.56 cm^{2} $,拼成的长方形的周长是(
16.56
)cm。
答案:
16.56
6. 如图,在平行四边形中,甲的面积是 $ 36 cm^{2} $,丙的面积是 $ 32 cm^{2} $,则乙的面积是(
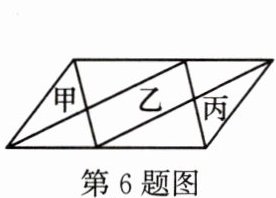
68
) $ cm^{2} $。
答案:
68
1. 一个长方形,长是 $ a $ m,宽是 $ b $ m,如果宽增加 5 m,面积增加(
A. $ 5a m^{2} $
B. $ 5b m^{2} $
C. $ 5ab m^{2} $
D. $ 25 m^{2} $
A
)。A. $ 5a m^{2} $
B. $ 5b m^{2} $
C. $ 5ab m^{2} $
D. $ 25 m^{2} $
答案:
A
2. 如右图中甲的面积是 42,乙的面积是 24,则丙的面积是(
A. 18
B. 66
C. 24
D. 42
D
)。A. 18
B. 66
C. 24
D. 42
答案:
D
3. 如右图中阴影部分面积的计算用(
A. 梯形面积
B. 小长方形面积+三角形面积
C. 大长方形面积-三角形面积
D. 把梯形转化成正方形
D
)计算方法最简便。A. 梯形面积
B. 小长方形面积+三角形面积
C. 大长方形面积-三角形面积
D. 把梯形转化成正方形
答案:
D
4. 有两个边长相等的正方形,在其中一个正方形里画 1 个最大的圆,另一个正方形里画 4 个相等的圆(如图)。下面说法中错误的是(
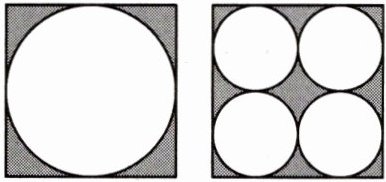
A. 两个正方形里空白部分的面积相等
B. 两个正方形里阴影部分的面积不相等
C. 大圆的周长小于四个小圆的周长和
B
)。
A. 两个正方形里空白部分的面积相等
B. 两个正方形里阴影部分的面积不相等
C. 大圆的周长小于四个小圆的周长和
答案:
B
5. 一个大圆的半径恰好是一个小圆的直径,这个小圆的面积是大圆面积的(
A. $ \frac{1}{2} $
B. $ (\frac{1}{2})^{2}×3.14 $
C. $ \frac{1}{8} $
D. $ \frac{1}{4} $
D
)。A. $ \frac{1}{2} $
B. $ (\frac{1}{2})^{2}×3.14 $
C. $ \frac{1}{8} $
D. $ \frac{1}{4} $
答案:
D
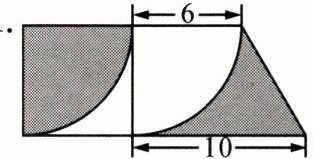
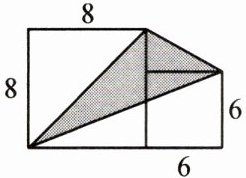
三、求下面各图形中阴影部分的面积。(单位:cm)
1.
2.
3. 长方形 $ABCD$ 中,$AB = 10$,$AE = 8$,$ED = 4$,且 $F$ 是线段 $BE$ 的中点,$G$ 是线段 $FC$ 的中点,求阴影部分面积。
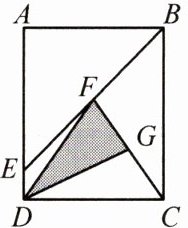
1.

(6 + 10)×6×\frac{1}{2} = 48(cm²)
2.

\frac{1}{2}×8×8 + 6×6 - (6 + 8)×6×\frac{1}{2} + \frac{1}{2}×6×2 = 32(cm²)
3. 长方形 $ABCD$ 中,$AB = 10$,$AE = 8$,$ED = 4$,且 $F$ 是线段 $BE$ 的中点,$G$ 是线段 $FC$ 的中点,求阴影部分面积。

连接 $AF$ $S_{长方形ABCD} = 10×(8 + 4) = 120$ $S_{△ABF} + S_{△CFD} = 120÷2 = 60$ $S_{△ABE} = 10×8÷2 = 40$ 因为 $F$ 是 $BE$ 的中点 所以 $S_{△ABF} = 40÷2 = 20$ 因为 $S_{△CFD} = 60 - 20 = 40$ 又因为 $G$ 是 $CF$ 的中点,所以 $S_{△DFG} = 40÷2 = 20$
答案:
1. $(6 + 10)×6×\frac{1}{2} = 48(cm^{2})$ 2. $\frac{1}{2}×8×8 + 6×6 - (6 + 8)×6×\frac{1}{2} + \frac{1}{2}×6×2 = 32(cm^{2})$ 3. 连接 $AF$ $S_{长方形ABCD} = 10×(8 + 4) = 120$ $S_{△ABF} + S_{△CFD} = 120÷2 = 60$ $S_{△ABE} = 10×8÷2 = 40$ 因为 $F$ 是 $BE$ 的中点 所以 $S_{△ABF} = 40÷2 = 20$ 因为 $S_{△CFD} = 60 - 20 = 40$ 又因为 $G$ 是 $CF$ 的中点,所以 $S_{△DFG} = 40÷2 = 20$
查看更多完整答案,请扫码查看


