《2025年暑假衔接起跑线小升初数学》

2. 一个高为 10 cm 的圆柱，如果它的高增加 2 cm，那么它的表面积就增加 125.6 cm²，求这个圆柱的体积。

答案： 底面半径：125.6 ÷ 2 ÷ 3.14 ÷ 2 = 10(cm) 体积：3.14 × 10² × 10 = 3140(cm³)

3. 一个圆柱形木桶装着水，在水中放一个底面积是木桶底面积的 $\frac{3}{5}$ 且高为 10 cm 的小圆锥，当小圆锥从桶中取出后，桶内的水面将下降多少厘米？

答案： 设圆柱底面积为 S cm²，水面下降 h cm 则有 Sh = $\frac{1}{3} × S × 10 × \frac{3}{5}$ Sh = 2S h = 2

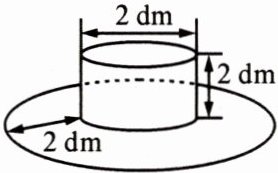
4. 下图是一顶帽子的示意图，帽顶部分是圆柱形，帽檐部分是一个圆环形，两部分的外面都是用同样的花布做成的，已知帽顶的直径和高及帽檐宽都是 2 dm，那么做这顶帽子，至少要用多少平方分米的花布？(最后结果保留整数)

(3.14 × 2 × 2 + 3.14 × (2 × 3 ÷ 2)² ≈ 41(dm²))

答案： 3.14 × 2 × 2 + 3.14 × (2 × 3 ÷ 2)² ≈ 41(dm²)

5. 下图表示一个正方体，它的棱长为 4 cm，在它的上下、前后、左右的正中位置各挖去一个棱长为 1 cm 的正方体。此图的表面积是多少？

(120cm²)

答案： 4 × 4 × 6 + 1 × 1 × 4 × 6 = 120(cm²)