2025年新课堂假期生活暑假用书八年级数学华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课堂假期生活暑假用书八年级数学华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3. 矩形具有而平行四边形不一定具有的特征是(
A. 对角线互相平分
B. 对角线相等
C. 两组对边平行且相等
D. 两组对角相等
B
)A. 对角线互相平分
B. 对角线相等
C. 两组对边平行且相等
D. 两组对角相等
答案:
B
1. 如图,在$\triangle ABC$中,$AB = AC$,$BC = 20cm$,点$P$在$BC$边上从点$B$开始以$2cm/s$的速度向点$C$运动,过点$P$作$PE// AC$交$AB$于点$E$,$PF// AB$交$AC$于点$F$. 请问四边形$AEPF$是否可能为菱形?若可能,是什么时刻?若不可能,请说明理由.
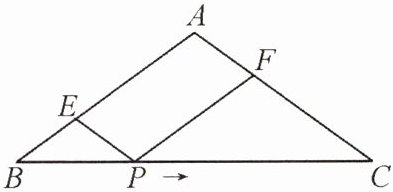
四边形$AEPF$

四边形$AEPF$
可能
为菱形,在5s
时。
答案:
【解析】:
因为$PE// AC$,$PF// AB$,所以四边形$AEPF$是平行四边形。
若四边形$AEPF$是菱形,则$AE = EP$。
因为$PE// AC$,所以$\angle EPB=\angle C$。
又因为$AB = AC$,所以$\angle B=\angle C$,则$\angle EPB=\angle B$,所以$BE = EP$,即$AE = BE$。
设运动时间为$t$秒,$BP = 2t$。
因为$AE = BE$,$PE// AC$,所以$BP = PC$。
已知$BC = 20cm$,则$2t=20\div2$,即$2t = 10$,解得$t = 5$。
【答案】:四边形$AEPF$可能为菱形,在$5s$时。
因为$PE// AC$,$PF// AB$,所以四边形$AEPF$是平行四边形。
若四边形$AEPF$是菱形,则$AE = EP$。
因为$PE// AC$,所以$\angle EPB=\angle C$。
又因为$AB = AC$,所以$\angle B=\angle C$,则$\angle EPB=\angle B$,所以$BE = EP$,即$AE = BE$。
设运动时间为$t$秒,$BP = 2t$。
因为$AE = BE$,$PE// AC$,所以$BP = PC$。
已知$BC = 20cm$,则$2t=20\div2$,即$2t = 10$,解得$t = 5$。
【答案】:四边形$AEPF$可能为菱形,在$5s$时。
2. 如图,已知在$Rt\triangle ABC$中,$∠ACB = 90^{\circ}$,$CD$是斜边$AB$的中线,$E$是边$BC$延长线上一点,连接$AE$,$DE$,过点$C$作$CF⊥DE$于点$F$,且$DF = EF$.
(1)求证:$AD = CE$.
(2)若$AD = 5$,$AC = 6$,求$\triangle BDE$的面积.
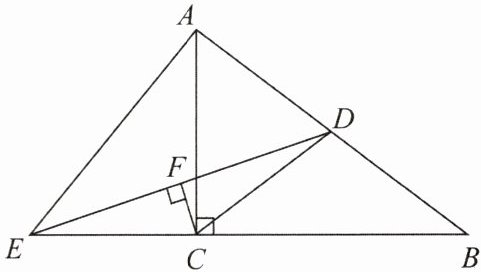
(1)求证:$AD = CE$.
(2)若$AD = 5$,$AC = 6$,求$\triangle BDE$的面积.
$\frac{39}{2}$

答案:
【解析】:
### (1)证明$AD = CE$
- 因为$CF\perp DE$且$DF = EF$,根据线段垂直平分线的性质,可知$CD = CE$。
- 在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD$是斜边$AB$的中线,根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,可得$CD = AD$。
- 所以$AD = CE$。
### (2)求$\triangle BDE$的面积
已知$AD = 5$,由(1)知$CD = AD = CE = 5$,所以$AB = 2AD = 10$。
在$Rt\triangle ABC$中,$AC = 6$,$AB = 10$,根据勾股定理$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}}=\sqrt{100 - 36}=\sqrt{64}=8$。
所以$BE=BC + CE=8 + 5=13$。
过$D$作$DH\perp BC$于$H$。
因为$D$是$AB$中点,$DH// AC$($\angle ACB = 90^{\circ}$,$DH\perp BC$),根据中位线定理,可得$DH=\frac{1}{2}AC$,$CH=\frac{1}{2}BC$。
所以$DH=\frac{1}{2}\times6 = 3$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),$\triangle BDE$的面积$S_{\triangle BDE}=\frac{1}{2}\times BE\times DH=\frac{1}{2}\times13\times3=\frac{39}{2}$。
【答案】:
(1) 证明过程如上述解析,证得$AD = CE$。
(2) $\triangle BDE$的面积为$\boldsymbol{\frac{39}{2}}$。
### (1)证明$AD = CE$
- 因为$CF\perp DE$且$DF = EF$,根据线段垂直平分线的性质,可知$CD = CE$。
- 在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD$是斜边$AB$的中线,根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,可得$CD = AD$。
- 所以$AD = CE$。
### (2)求$\triangle BDE$的面积
已知$AD = 5$,由(1)知$CD = AD = CE = 5$,所以$AB = 2AD = 10$。
在$Rt\triangle ABC$中,$AC = 6$,$AB = 10$,根据勾股定理$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}}=\sqrt{100 - 36}=\sqrt{64}=8$。
所以$BE=BC + CE=8 + 5=13$。
过$D$作$DH\perp BC$于$H$。
因为$D$是$AB$中点,$DH// AC$($\angle ACB = 90^{\circ}$,$DH\perp BC$),根据中位线定理,可得$DH=\frac{1}{2}AC$,$CH=\frac{1}{2}BC$。
所以$DH=\frac{1}{2}\times6 = 3$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),$\triangle BDE$的面积$S_{\triangle BDE}=\frac{1}{2}\times BE\times DH=\frac{1}{2}\times13\times3=\frac{39}{2}$。
【答案】:
(1) 证明过程如上述解析,证得$AD = CE$。
(2) $\triangle BDE$的面积为$\boldsymbol{\frac{39}{2}}$。
3. 如图,在正方形$ABCD$外有一点$P$,$AP = AD$,$∠PAD = 40^{\circ}$,求$∠PBC$与$∠BPD$的度数.
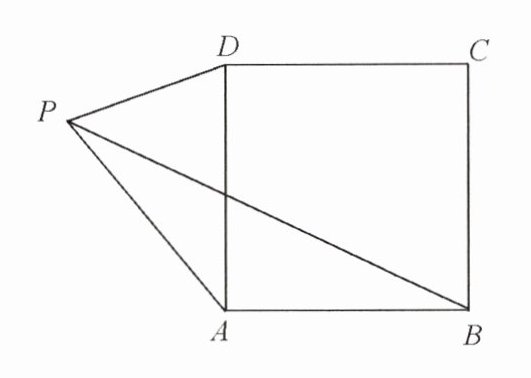
$∠PBC=$

$∠PBC=$
$65^{\circ}$
,$∠BPD=$$45^{\circ}$
答案:
$\angle PBC = 65^{\circ}$,$\angle BPD = 45^{\circ}$
查看更多完整答案,请扫码查看


