《2025年新课堂假期生活暑假用书八年级数学华师大版》

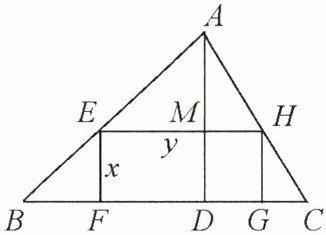
3. 如图，在△ABC 中，BC = 10，高 AD = 6，四边形 EFGH 是它的内接矩形，设 EF 为 x，EH 为 y，求 y 关于 x 的函数关系式，并确定自变量 x 的取值范围.

函数关系式为$y = -\frac{5}{3}x + 10$，自变量 x 的取值范围是$0＜x＜6$.

答案： 【解析】：
因为四边形$EFGH$是矩形，所以$EH// BC$，则$\triangle AEH\sim\triangle ABC$。
由相似三角形对应高的比等于相似比，可得$\frac{AM}{AD}=\frac{EH}{BC}$。
已知$EF = x$，$AD = 6$，所以$AM = 6 - x$，又$BC = 10$，$EH = y$，代入可得$\frac{6 - x}{6}=\frac{y}{10}$。
化简这个等式：
$\begin{aligned}10\times(6 - x)&=6y\\60 - 10x&=6y\\y&=\frac{60 - 10x}{6}\\y&=-\frac{5}{3}x + 10\end{aligned}$
因为$EF$是矩形的边且长度大于$0$，同时$AM = 6 - x＞0$（$AM$为线段长度大于$0$），所以$0＜x＜6$。
【答案】：$y = -\frac{5}{3}x + 10$，自变量$x$的取值范围是$0＜x＜6$。

4. 已知等腰三角形的周长为 10 cm，腰长为 x cm，底边长为 y cm.
(1)以腰长 x 为自变量，写出 y 与 x 的函数表达式，并求自变量 x 的取值范围；
(2)当 y = 3 时，求 x 的值；
(3)画出函数的图象.

答案： 【解析】：
1. （1）根据等腰三角形周长公式：周长 = 腰长×2 + 底边长，已知等腰三角形周长为$10cm$，腰长为$x cm$，底边长为$y cm$，可得$2x + y = 10$，移项可得$y$与$x$的函数表达式为$y = 10 - 2x$。
根据三角形三边关系：任意两边之和大于第三边，可得$2x＞y$，即$2x＞10 - 2x$，解这个不等式：
$2x+2x＞10$，$4x＞10$，$x ＞ 2.5$；
又因为边长$y=10 - 2x＞0$，解这个不等式：
$10＞2x$，$x ＜ 5$。
所以自变量$x$的取值范围是$2.5 ＜ x ＜ 5$。
2. （2）当$y = 3$时，把$y = 3$代入$y = 10 - 2x$中，得到$3 = 10 - 2x$，移项可得$2x = 10 - 3$，即$2x = 7$，解得$x = 3.5$。
3. （3）对于函数$y = 10 - 2x(2.5 ＜ x ＜ 5)$，
当$x = 2.5$时，$y = 10 - 2×2.5=10 - 5 = 5$；当$x = 5$时，$y = 10 - 2×5 = 0$。
因为$x$的取值范围是$2.5 ＜ x ＜ 5$，所以函数图象是一条线段，端点分别为$(2.5,5)$和$(5,0)$，但这两个端点是空心的。先建立平面直角坐标系，在$x$轴上找到$2.5$和$5$的位置，在$y$轴上找到$5$和$0$的位置，然后用空心圆圈标记点$(2.5,5)$和$(5,0)$，最后连接这两个空心点得到线段。
【答案】：
1. $y = 10 - 2x(2.5 ＜ x ＜ 5)$
2. $x = 3.5$
3. 函数图象是一条线段，端点分别为$(2.5,5)$和$(5,0)$（端点为空心），建立平面直角坐标系，用空心圆圈标记点$(2.5,5)$和$(5,0)$，连接这两个空心点得到线段。