2025年新课堂假期生活暑假用书八年级数学华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课堂假期生活暑假用书八年级数学华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使 $ AB = CD $,$ EF = GH $;
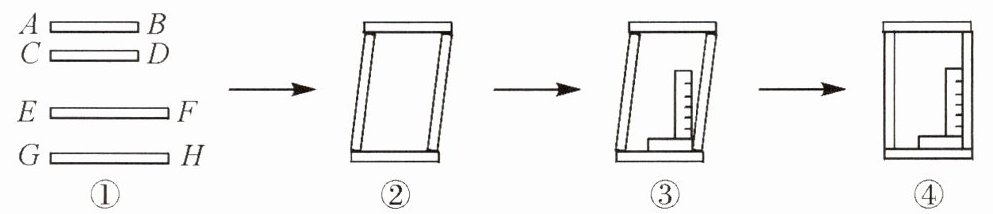
(2)摆放成如图②的四边形,则这时窗框的形状是
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是
(1)先截出两对符合规格的铝合金窗料(如图①),使 $ AB = CD $,$ EF = GH $;

(2)摆放成如图②的四边形,则这时窗框的形状是
平行四边
形,根据的数学道理是两组对边分别相等的四边形是平行四边形
;(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是
矩
形,根据的数学道理是有一个角是直角的平行四边形是矩形
。
答案:
(2) 平行四边;两组对边分别相等的四边形是平行四边形
(3) 矩;有一个角是直角的平行四边形是矩形
(2) 平行四边;两组对边分别相等的四边形是平行四边形
(3) 矩;有一个角是直角的平行四边形是矩形
2. 矩形的两条对角线的夹角为 $ 60^{\circ} $。
(1)若较短边长为 $ 3.6 \mathrm{~cm} $,则对角线长为
(2)若一条对角线与较短边的和为 $ 15 \mathrm{~cm} $,则较短边的长为
(1)若较短边长为 $ 3.6 \mathrm{~cm} $,则对角线长为
7.2
$ \mathrm{cm} $;(2)若一条对角线与较短边的和为 $ 15 \mathrm{~cm} $,则较短边的长为
5
$ \mathrm{cm} $。
答案:
1. $7.2$ 2. $5$
3. 如果菱形的边长是 $ 2 \mathrm{~cm} $,那么菱形的周长是
8
$ \mathrm{cm} $;如果菱形的边长与一条对角线的长相等,那么这个菱形的相邻两内角的度数分别是60°
和120°
。
答案:
1. $8$ 2. $60^{\circ}$ 3. $120^{\circ}$
4. 已知一个正方形的对角线长为 $ 10 \mathrm{~cm} $,则这个正方形的面积为
50
$ \mathrm{cm}^{2} $。
答案:
$50$
5. 以正方形 $ ABCD $ 的边 $ AB $ 为边作等边三角形 $ ABE $,则 $ \angle DAE $ 的度数为
$30^{\circ}$或$150^{\circ}$
。
答案:
$30^{\circ}$或$150^{\circ}$
1. 如图,矩形 $ ABCD $ 的两条对角线相交于点 $ O $,$ \angle AOD = 120^{\circ} $,$ AB = 6 \mathrm{~cm} $,求 $ AC $ 的长。


12cm
答案:
【解析】:
- 因为四边形$ABCD$是矩形,根据矩形的性质:矩形的对角线相等且互相平分,所以$AC = BD$,$OA=\frac{1}{2}AC$,$OD=\frac{1}{2}BD$,则$OA = OD$。
- 已知$\angle AOD = 120^{\circ}$,那么$\angle AOB=180^{\circ}-\angle AOD = 180^{\circ}- 120^{\circ}=60^{\circ}$。
- 又因为$OA = OB$(由矩形对角线性质得出),所以$\triangle AOB$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形)。
- 因为$AB = 6\mathrm{cm}$,且$\triangle AOB$是等边三角形,所以$OA=AB = 6\mathrm{cm}$。
- 而$AC = 2OA$,所以$AC=2\times6 = 12\mathrm{cm}$。
【答案】:$12\mathrm{cm}$
- 因为四边形$ABCD$是矩形,根据矩形的性质:矩形的对角线相等且互相平分,所以$AC = BD$,$OA=\frac{1}{2}AC$,$OD=\frac{1}{2}BD$,则$OA = OD$。
- 已知$\angle AOD = 120^{\circ}$,那么$\angle AOB=180^{\circ}-\angle AOD = 180^{\circ}- 120^{\circ}=60^{\circ}$。
- 又因为$OA = OB$(由矩形对角线性质得出),所以$\triangle AOB$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形)。
- 因为$AB = 6\mathrm{cm}$,且$\triangle AOB$是等边三角形,所以$OA=AB = 6\mathrm{cm}$。
- 而$AC = 2OA$,所以$AC=2\times6 = 12\mathrm{cm}$。
【答案】:$12\mathrm{cm}$
查看更多完整答案,请扫码查看


