《2025年新课堂假期生活暑假用书八年级数学华师大版》

4. 两条平行线被第三条直线所截，两组内错角的平分线围成的四边形是（C）
A. 一般的四边形
B. 一般的平行四边形
C. 矩形
D. 梯形

答案： C

5. 如果菱形的对角线长分别为$12$和$16$，那么它的面积为（C）
A. $48$
B. $50\sqrt{3}$
C. $96$
D. $82$

答案： C

1. 如图，在$□ ABCD$中，$DE\perp AB$于点$E$，$DF\perp BC$于点$F$，$□ ABCD$的周长是$36$，$DE=4\sqrt{3}$，$DF=5\sqrt{3}$。求：
（1）$AD$、$CD$的长；$AD = 8$，$CD = 10$
（2）$\angle A$、$\angle B$的度数。$\angle A = 60^{\circ}$，$\angle B = 120^{\circ}$

答案： 【解析】：
1. 首先根据平行四边形的性质和周长公式：
因为四边形$ABCD$是平行四边形，所以$AB = CD$，$AD = BC$。已知平行四边形$ABCD$的周长是$36$，则$2(AB + AD)=36$，即$AB + AD = 18$，设$AB=x$，$AD = y$，那么$x + y=18$。
根据平行四边形的面积公式$S = AB\times DE=BC\times DF$（平行四边形面积可以用一边乘以这边上的高来计算），已知$DE = 4\sqrt{3}$，$DF = 5\sqrt{3}$，所以$4\sqrt{3}x=5\sqrt{3}y$，即$4x = 5y$。
联立方程组$\begin{cases}x + y=18\\4x = 5y\end{cases}$，由$x + y=18$可得$x = 18 - y$，将其代入$4x = 5y$中，得到$4(18 - y)=5y$。
展开括号得$72-4y = 5y$，移项可得$5y + 4y=72$，即$9y = 72$，解得$y = 8$。
把$y = 8$代入$x = 18 - y$，得$x = 10$。所以$AD = 8$，$CD = 10$。
2. 然后求$\angle A$和$\angle B$的度数：
在$Rt\triangle ADE$中，$\sin A=\frac{DE}{AD}$，已知$DE = 4\sqrt{3}$，$AD = 8$，则$\sin A=\frac{4\sqrt{3}}{8}=\frac{\sqrt{3}}{2}$。
因为$0^{\circ}\lt\angle A\lt180^{\circ}$，所以$\angle A = 60^{\circ}$。
由于平行四边形$ABCD$中$AD// BC$，根据两直线平行，同旁内角互补，所以$\angle A+\angle B = 180^{\circ}$，则$\angle B=180^{\circ}-\angle A = 120^{\circ}$。
【答案】：1. $AD = 8$，$CD = 10$ 2. $\angle A = 60^{\circ}$，$\angle B = 120^{\circ}$

2. 如图，在菱形$ABCD$中，$AB=4\mathrm{cm}$，高$AE$平分$BC$。求：
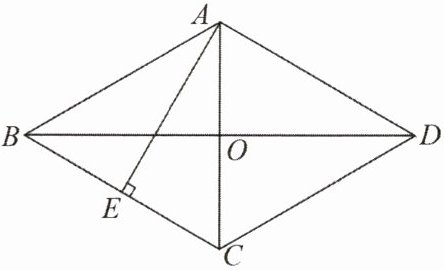
（1）菱形$ABCD$的面积为$8\sqrt{3}cm^{2}$；
（2）对角线$BD$的长为$4\sqrt{3}cm$。

答案： （1）$8\sqrt{3}cm^{2}$ （2）$4\sqrt{3}cm$