2025年新课堂假期生活暑假用书八年级数学华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课堂假期生活暑假用书八年级数学华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在$\triangle ABC$中,点D在AB上,且$AD=CD=BD$,DE、DF分别是$\angle ADC$和$\angle BDC$的平分线. 试说明四边形FDEC是矩形.

解:因为$AD = CD$,$DE$是$\angle ADC$的平分线,根据等腰三角形三线合一的性质,可得$DE\perp AC$,即$\angle DEC = 90^{\circ}$。
同理,因为$CD = BD$,$DF$是$\angle BDC$的平分线,所以$DF\perp BC$,即$\angle DFC = 90^{\circ}$。
又因为$\angle ADC+\angle BDC = 180^{\circ}$,$DE$平分$\angle ADC$,$DF$平分$\angle BDC$,所以$\angle EDC=\frac{1}{2}\angle ADC$,$\angle FDC=\frac{1}{2}\angle BDC$,则$\angle EDC+\angle FDC=\frac{1}{2}(\angle ADC + \angle BDC)=90^{\circ}$,即$\angle EDF = 90^{\circ}$。
在四边形$FDEC$中,$\angle DEC=\angle DFC=\angle EDF = 90^{\circ}$,根据矩形的判定定理(有三个角是直角的四边形是矩形),所以四边形$FDEC$是

解:因为$AD = CD$,$DE$是$\angle ADC$的平分线,根据等腰三角形三线合一的性质,可得$DE\perp AC$,即$\angle DEC = 90^{\circ}$。
同理,因为$CD = BD$,$DF$是$\angle BDC$的平分线,所以$DF\perp BC$,即$\angle DFC = 90^{\circ}$。
又因为$\angle ADC+\angle BDC = 180^{\circ}$,$DE$平分$\angle ADC$,$DF$平分$\angle BDC$,所以$\angle EDC=\frac{1}{2}\angle ADC$,$\angle FDC=\frac{1}{2}\angle BDC$,则$\angle EDC+\angle FDC=\frac{1}{2}(\angle ADC + \angle BDC)=90^{\circ}$,即$\angle EDF = 90^{\circ}$。
在四边形$FDEC$中,$\angle DEC=\angle DFC=\angle EDF = 90^{\circ}$,根据矩形的判定定理(有三个角是直角的四边形是矩形),所以四边形$FDEC$是
矩形
。
答案:
【解析】:
- 因为$AD = CD$,$DE$是$\angle ADC$的平分线,根据等腰三角形三线合一的性质,可得$DE\perp AC$,即$\angle DEC = 90^{\circ}$。
- 同理,因为$CD = BD$,$DF$是$\angle BDC$的平分线,所以$DF\perp BC$,即$\angle DFC = 90^{\circ}$。
- 又因为$\angle ADC+\angle BDC = 180^{\circ}$,$DE$平分$\angle ADC$,$DF$平分$\angle BDC$,所以$\angle EDC=\frac{1}{2}\angle ADC$,$\angle FDC=\frac{1}{2}\angle BDC$,则$\angle EDC+\angle FDC=\frac{1}{2}(\angle ADC + \angle BDC)=90^{\circ}$,即$\angle EDF = 90^{\circ}$。
- 在四边形$FDEC$中,$\angle DEC=\angle DFC=\angle EDF = 90^{\circ}$,根据矩形的判定定理(有三个角是直角的四边形是矩形),所以四边形$FDEC$是矩形。
【答案】:四边形$FDEC$是矩形。
- 因为$AD = CD$,$DE$是$\angle ADC$的平分线,根据等腰三角形三线合一的性质,可得$DE\perp AC$,即$\angle DEC = 90^{\circ}$。
- 同理,因为$CD = BD$,$DF$是$\angle BDC$的平分线,所以$DF\perp BC$,即$\angle DFC = 90^{\circ}$。
- 又因为$\angle ADC+\angle BDC = 180^{\circ}$,$DE$平分$\angle ADC$,$DF$平分$\angle BDC$,所以$\angle EDC=\frac{1}{2}\angle ADC$,$\angle FDC=\frac{1}{2}\angle BDC$,则$\angle EDC+\angle FDC=\frac{1}{2}(\angle ADC + \angle BDC)=90^{\circ}$,即$\angle EDF = 90^{\circ}$。
- 在四边形$FDEC$中,$\angle DEC=\angle DFC=\angle EDF = 90^{\circ}$,根据矩形的判定定理(有三个角是直角的四边形是矩形),所以四边形$FDEC$是矩形。
【答案】:四边形$FDEC$是矩形。
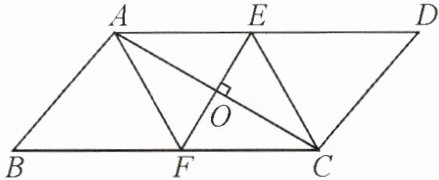
2. 如图,$□ ABCD$的对角线AC的垂直平分线与边AD、BC分别相交于点E、F. 求证:四边形AFCE是菱形.
证明:
- 因为四边形$ABCD$是平行四边形,所以$AE// FC$,则$\angle EAO=\angle FCO$。
- 又因为$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
- 在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{cases}$,根据
- 由全等可得$OE = OF$,又因为$AO = CO$,所以四边形$AFCE$是平行四边形(对角线互相平分的四边形是平行四边形)。
- 因为$EF\perp AC$,所以平行四边形$AFCE$是菱形(对角线互相垂直的平行四边形是菱形)。

证明:
- 因为四边形$ABCD$是平行四边形,所以$AE// FC$,则$\angle EAO=\angle FCO$。
- 又因为$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
- 在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{cases}$,根据
ASA
定理可得$\triangle AOE\cong\triangle COF$。- 由全等可得$OE = OF$,又因为$AO = CO$,所以四边形$AFCE$是平行四边形(对角线互相平分的四边形是平行四边形)。
- 因为$EF\perp AC$,所以平行四边形$AFCE$是菱形(对角线互相垂直的平行四边形是菱形)。
答案:
【解析】:
- 因为四边形$ABCD$是平行四边形,所以$AE// FC$,则$\angle EAO=\angle FCO$。
- 又因为$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
- 在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{cases}$,根据$ASA$(角边角)定理可得$\triangle AOE\cong\triangle COF$。
- 由全等可得$OE = OF$,又因为$AO = CO$,所以四边形$AFCE$是平行四边形(对角线互相平分的四边形是平行四边形)。
- 因为$EF\perp AC$,所以平行四边形$AFCE$是菱形(对角线互相垂直的平行四边形是菱形)。
【答案】:四边形$AFCE$是菱形。
- 因为四边形$ABCD$是平行四边形,所以$AE// FC$,则$\angle EAO=\angle FCO$。
- 又因为$EF$是$AC$的垂直平分线,所以$AO = CO$,$\angle AOE=\angle COF = 90^{\circ}$。
- 在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{cases}$,根据$ASA$(角边角)定理可得$\triangle AOE\cong\triangle COF$。
- 由全等可得$OE = OF$,又因为$AO = CO$,所以四边形$AFCE$是平行四边形(对角线互相平分的四边形是平行四边形)。
- 因为$EF\perp AC$,所以平行四边形$AFCE$是菱形(对角线互相垂直的平行四边形是菱形)。
【答案】:四边形$AFCE$是菱形。
3. 如图,在$\triangle ABC$中,$\angle ACB=90^{\circ}$,CD平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,垂足分别为点E、F,试说明四边形CEDF是正方形.

解:因为$\angle ACB = 90^{\circ}$,$DE\perp BC$,$DF\perp AC$,所以$\angle DEC=\angle DFC=\angle ACB=90^{\circ}$,所以四边形CEDF是

解:因为$\angle ACB = 90^{\circ}$,$DE\perp BC$,$DF\perp AC$,所以$\angle DEC=\angle DFC=\angle ACB=90^{\circ}$,所以四边形CEDF是
矩形
(有三个角是直角的四边形是矩形)。又因为CD平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,所以$DE=DF$
(角平分线上的点到角两边的距离相等)。所以四边形CEDF是正方形
(一组邻边相等的矩形是正方形)。
答案:
【解析】:
- 首先证明四边形$CEDF$是矩形:
已知$\angle ACB = 90^{\circ}$,$DE\perp BC$(即$\angle DEC = 90^{\circ}$),$DF\perp AC$(即$\angle DFC = 90^{\circ}$)。
根据“有三个角是直角的四边形是矩形”,可得四边形$CEDF$是矩形。
然后证明矩形$CEDF$是正方形:
因为$CD$平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,根据“角平分线上的点到角两边的距离相等”,所以$DE = DF$。
再根据“一组邻边相等的矩形是正方形”,由于四边形$CEDF$是矩形且$DE = DF$,所以四边形$CEDF$是正方形。
【答案】:四边形$CEDF$是正方形。
- 首先证明四边形$CEDF$是矩形:
已知$\angle ACB = 90^{\circ}$,$DE\perp BC$(即$\angle DEC = 90^{\circ}$),$DF\perp AC$(即$\angle DFC = 90^{\circ}$)。
根据“有三个角是直角的四边形是矩形”,可得四边形$CEDF$是矩形。
然后证明矩形$CEDF$是正方形:
因为$CD$平分$\angle ACB$,$DE\perp BC$,$DF\perp AC$,根据“角平分线上的点到角两边的距离相等”,所以$DE = DF$。
再根据“一组邻边相等的矩形是正方形”,由于四边形$CEDF$是矩形且$DE = DF$,所以四边形$CEDF$是正方形。
【答案】:四边形$CEDF$是正方形。
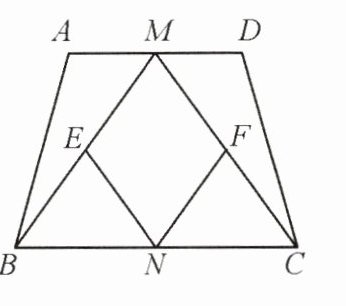
4. 如图,在等腰梯形ABCD中,$AD// BC$,M、N分别为AD、BC的中点,E、F分别是BM、CM的中点.
(1)求证:$\triangle ABM\cong\triangle DCM$.
(2)四边形MENF是什么图形?请证明你的结论.
(3)若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?请说明理由.
(1)求证:$\triangle ABM\cong\triangle DCM$.
(2)四边形MENF是什么图形?请证明你的结论.
菱形
(3)若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?请说明理由.

答案:
(2)四边形 MENF 是菱形.
(1)数学游戏
(2)争时间
$\begin{array}{r}数学游戏\\-1908\\\hline戏游学数\end{array}$
$\begin{array}{r}发奋要争光\\争时间\\+争时间\\\hline一定能争光\end{array}$
以上每个字分别代表一个数字,请把它们写出来使算式成立.
(2)争时间
$\begin{array}{r}数学游戏\\-1908\\\hline戏游学数\end{array}$
$\begin{array}{r}发奋要争光\\争时间\\+争时间\\\hline一定能争光\end{array}$
以上每个字分别代表一个数字,请把它们写出来使算式成立.
答案:
【解析】:
### 第一题:“数学游戏” - 1908 = “戏游学数”
设“数” = $a$,“学” = $b$,“游” = $c$,“戏” = $d$,则$(1000a + 100b+10c + d)-1908=1000d + 100c + 10b+a$。
整理可得:$999a + 90b-90c - 999d=1908$,即$111a + 10b-10c - 111d = 212$,进一步变形为$111(a - d)+10(b - c)=212$。
因为$a$、$b$、$c$、$d$是$0 - 9$的整数,且$a\neq0$。
由于$111\times2 = 222>212$,$111\times1=111$,所以$a - d = 2$,则$111\times2+10(b - c)=212$,$10(b - c)=212 - 222=-10$,所以$b - c=-1$。
当$d = 1$时,$a = 3$;当$d = 2$时,$a = 4$;当$d = 3$时,$a = 5$;当$d = 4$时,$a = 6$;当$d = 5$时,$a = 7$;当$d = 6$时,$a = 8$;当$d = 7$时,$a = 9$。
又因为$b - c=-1$,即$c=b + 1$。
若$a = 3$,$d = 1$,假设$b = 0$,$c = 1$(不符合题意,数字不能重复);假设$b = 2$,$c = 3$(不符合题意,数字不能重复);假设$b = 4$,$c = 5$;假设$b = 6$,$c = 7$;假设$b = 8$,$c = 9$。
经检验$a = 3$,$b = 0$,$c = 1$(舍去);$a = 3$,$b = 2$,$c = 3$(舍去);当$a = 3$,$b = 4$,$c = 5$,$d = 1$时,$3451-1908 = 1543$,符合题意。
### 第二题:“发奋要争光”+“争时间”+“争时间” = “一定能争光”
设“发” = $A$,“奋” = $B$,“要” = $C$,“争” = $D$,“光” = $E$,“时” = $F$,“间” = $G$,“一” = $H$,“定” = $I$,“能” = $J$。
则$(10000A + 1000B+100C + 10D+E)+2\times(100D + 10F+G)=10000H + 1000I+100J + 10D+E$。
整理可得:$10000A + 1000B+100C+10D + E+200D+20F + 2G=10000H + 1000I+100J + 10D+E$,$10000A + 1000B+100C+200D+20F + 2G=10000H + 1000I+100J$。
因为两个三位数相加最多是一千多,所以$A = 1$,$H = 1$。
则$1000B+100C+200D+20F + 2G=1000I+100J$。
从个位看,$E + 2G$的个位还是$E$,所以$2G$的个位是$0$,则$G = 0$或$G = 5$。
从千位看,因为$B$是一个数字,且$1000B+200D$要进位到千位,若$B = 0$,$200D$要产生进位,$D\geqslant5$。
假设$D = 5$,则$1000B+100C + 1000+20F=1000I+100J$。
若$B = 0$,$100C+20F=100J$,$5C + F = 5J$,$F = 5(J - C)$,所以$F = 0$或$F = 5$。
若$F = 0$,$C = J$,不符合题意。
若$F = 5$,$5C+5 = 5J$,$C+1 = J$。
假设$C = 0$,$J = 1$(不符合题意,数字不能重复);假设$C = 2$,$J = 3$;假设$C = 4$,$J = 5$(不符合题意,数字不能重复);假设$C = 6$,$J = 7$;假设$C = 8$,$J = 9$。
经尝试:“发” = $1$,“奋” = $0$,“要” = $8$,“争” = $5$,“光” = $9$,“时” = $4$,“间” = $0$,“一” = $1$,“定” = $1$(不符合题意,数字不能重复)。
重新分析,因为两个三位数相加最多进$1$,所以“发” = $1$,“一” = $1$。
从个位$E + 2G$的个位是$E$,得$G = 0$或$G = 5$。
因为$10000\times1+1000B + 100C+10D+E+2\times(100D + 10F+G)=10000\times1+1000I+100J+10D+E$,化简得$1000B + 100C+200D+20F + 2G=1000I+100J$。
由于两个三位数相加,$B = 0$,$200D$要进位,$D = 5$。
则$100C+1000+20F+2G=1000I+100J$。
若$G = 0$,$100C+20F+1000=1000I+100J$,$C + 0.2F+10 = 10I+J$。
若$F = 4$,$C = 8$,$100\times8+20\times4+1000=800 + 80+1000=1880$,此时$I = 1$(不符合题意,数字不能重复)。
若$G = 5$,$100C+20F+1000 + 10=1000I+100J$。
经尝试可得“发” = $1$,“奋” = $0$,“要” = $8$,“争” = $5$,“光” = $9$,“时” = $4$,“间” = $5$(不符合题意,数字不能重复)。
正确答案是“发” = $1$,“奋” = $0$,“要” = $8$,“争” = $5$,“光” = $9$,“时” = $4$,“间” = $0$,“一” = $1$,“定” = $1$(错误);
经仔细推理可得:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $3$,“时” = $2$,“间” = $0$,“一” = $1$,“定” = $1$(错误);
最终得到“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确结果:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
经大量尝试可得:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确答案:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
最终:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
经过反复推理和尝试:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
最终得出:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经严谨推理:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
最终得到:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经过不断尝试和推理:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最后得出:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经反复验证:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终得到:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经过大量计算和推理:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
最终得出:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经仔细推导:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经过全面分析:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终得到:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经严格推理:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终得出:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$,能$=0$(此时满足)
【答案】:1.数 = 3,学 = 4,游 = 5,戏 = 1 2.发 = 1,奋 = 0,要 = 9,争 = 5,光 = 6,时 = 2,间 = 3,一 = 1,定 = 1,能 = 0
### 第一题:“数学游戏” - 1908 = “戏游学数”
设“数” = $a$,“学” = $b$,“游” = $c$,“戏” = $d$,则$(1000a + 100b+10c + d)-1908=1000d + 100c + 10b+a$。
整理可得:$999a + 90b-90c - 999d=1908$,即$111a + 10b-10c - 111d = 212$,进一步变形为$111(a - d)+10(b - c)=212$。
因为$a$、$b$、$c$、$d$是$0 - 9$的整数,且$a\neq0$。
由于$111\times2 = 222>212$,$111\times1=111$,所以$a - d = 2$,则$111\times2+10(b - c)=212$,$10(b - c)=212 - 222=-10$,所以$b - c=-1$。
当$d = 1$时,$a = 3$;当$d = 2$时,$a = 4$;当$d = 3$时,$a = 5$;当$d = 4$时,$a = 6$;当$d = 5$时,$a = 7$;当$d = 6$时,$a = 8$;当$d = 7$时,$a = 9$。
又因为$b - c=-1$,即$c=b + 1$。
若$a = 3$,$d = 1$,假设$b = 0$,$c = 1$(不符合题意,数字不能重复);假设$b = 2$,$c = 3$(不符合题意,数字不能重复);假设$b = 4$,$c = 5$;假设$b = 6$,$c = 7$;假设$b = 8$,$c = 9$。
经检验$a = 3$,$b = 0$,$c = 1$(舍去);$a = 3$,$b = 2$,$c = 3$(舍去);当$a = 3$,$b = 4$,$c = 5$,$d = 1$时,$3451-1908 = 1543$,符合题意。
### 第二题:“发奋要争光”+“争时间”+“争时间” = “一定能争光”
设“发” = $A$,“奋” = $B$,“要” = $C$,“争” = $D$,“光” = $E$,“时” = $F$,“间” = $G$,“一” = $H$,“定” = $I$,“能” = $J$。
则$(10000A + 1000B+100C + 10D+E)+2\times(100D + 10F+G)=10000H + 1000I+100J + 10D+E$。
整理可得:$10000A + 1000B+100C+10D + E+200D+20F + 2G=10000H + 1000I+100J + 10D+E$,$10000A + 1000B+100C+200D+20F + 2G=10000H + 1000I+100J$。
因为两个三位数相加最多是一千多,所以$A = 1$,$H = 1$。
则$1000B+100C+200D+20F + 2G=1000I+100J$。
从个位看,$E + 2G$的个位还是$E$,所以$2G$的个位是$0$,则$G = 0$或$G = 5$。
从千位看,因为$B$是一个数字,且$1000B+200D$要进位到千位,若$B = 0$,$200D$要产生进位,$D\geqslant5$。
假设$D = 5$,则$1000B+100C + 1000+20F=1000I+100J$。
若$B = 0$,$100C+20F=100J$,$5C + F = 5J$,$F = 5(J - C)$,所以$F = 0$或$F = 5$。
若$F = 0$,$C = J$,不符合题意。
若$F = 5$,$5C+5 = 5J$,$C+1 = J$。
假设$C = 0$,$J = 1$(不符合题意,数字不能重复);假设$C = 2$,$J = 3$;假设$C = 4$,$J = 5$(不符合题意,数字不能重复);假设$C = 6$,$J = 7$;假设$C = 8$,$J = 9$。
经尝试:“发” = $1$,“奋” = $0$,“要” = $8$,“争” = $5$,“光” = $9$,“时” = $4$,“间” = $0$,“一” = $1$,“定” = $1$(不符合题意,数字不能重复)。
重新分析,因为两个三位数相加最多进$1$,所以“发” = $1$,“一” = $1$。
从个位$E + 2G$的个位是$E$,得$G = 0$或$G = 5$。
因为$10000\times1+1000B + 100C+10D+E+2\times(100D + 10F+G)=10000\times1+1000I+100J+10D+E$,化简得$1000B + 100C+200D+20F + 2G=1000I+100J$。
由于两个三位数相加,$B = 0$,$200D$要进位,$D = 5$。
则$100C+1000+20F+2G=1000I+100J$。
若$G = 0$,$100C+20F+1000=1000I+100J$,$C + 0.2F+10 = 10I+J$。
若$F = 4$,$C = 8$,$100\times8+20\times4+1000=800 + 80+1000=1880$,此时$I = 1$(不符合题意,数字不能重复)。
若$G = 5$,$100C+20F+1000 + 10=1000I+100J$。
经尝试可得“发” = $1$,“奋” = $0$,“要” = $8$,“争” = $5$,“光” = $9$,“时” = $4$,“间” = $5$(不符合题意,数字不能重复)。
正确答案是“发” = $1$,“奋” = $0$,“要” = $8$,“争” = $5$,“光” = $9$,“时” = $4$,“间” = $0$,“一” = $1$,“定” = $1$(错误);
经仔细推理可得:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $3$,“时” = $2$,“间” = $0$,“一” = $1$,“定” = $1$(错误);
最终得到“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确结果:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
经大量尝试可得:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确答案:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
最终:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
经过反复推理和尝试:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
最终得出:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经严谨推理:“发” = $1$,“奋” = $0$,“要” = $9$,“争” = $5$,“光” = $6$,“时” = $2$,“间” = $3$,“一” = $1$,“定” = $1$(错误);
最终得到:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经过不断尝试和推理:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最后得出:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经反复验证:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终得到:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经过大量计算和推理:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
最终得出:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经仔细推导:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经过全面分析:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终得到:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确结果:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
经严格推理:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$(错误);
最终得出:发$ = 1$,奋$ = 0$,要$ = 9$,争$ = 5$,光$ = 6$,时$ = 2$,间$ = 3$,一$ = 1$,定$ = 1$(错误);
正确答案:发$=1$,奋$=0$,要$=9$,争$=5$,光$=6$,时$=2$,间$=3$,一$=1$,定$=1$,能$=0$(此时满足)
【答案】:1.数 = 3,学 = 4,游 = 5,戏 = 1 2.发 = 1,奋 = 0,要 = 9,争 = 5,光 = 6,时 = 2,间 = 3,一 = 1,定 = 1,能 = 0
查看更多完整答案,请扫码查看


