《2025年新课堂假期生活暑假用书八年级数学华师大版》

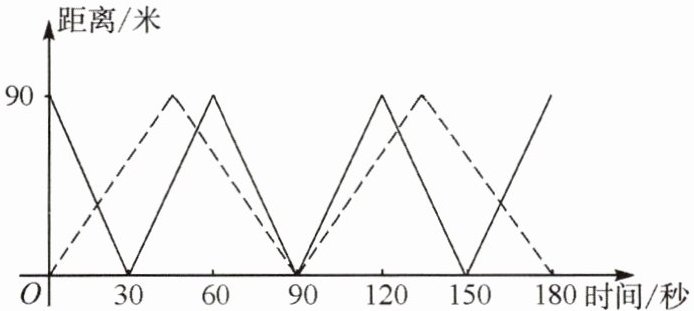
2. 一游泳池长$90$米，甲、乙二人分别在游泳池相对两边同时朝另一边游，甲的速度是$3$米/秒，乙的速度是$2$米/秒，图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化的图象. 若不计转向时间，则从开始起到$3$分钟止，他们相遇5次？

答案： 5次

3. 已知点$A(3,4)$，$B(-3,4)$，则以点$A$，$B$和原点$O$为顶点的三角形是什么三角形？它的面积为多少？

答案： 【解析】：首先，根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$，计算$OA$的长度，$O(0,0)$，$A(3,4)$，则$OA=\sqrt{(3 - 0)^2+(4 - 0)^2}=\sqrt{9 + 16}=\sqrt{25}=5$；计算$OB$的长度，$O(0,0)$，$B(-3,4)$，则$OB=\sqrt{(-3 - 0)^2+(4 - 0)^2}=\sqrt{9 + 16}=\sqrt{25}=5$；计算$AB$的长度，$A(3,4)$，$B(-3,4)$，则$AB=\sqrt{(-3 - 3)^2+(4 - 4)^2}=\sqrt{(-6)^2}=6$。因为$OA = OB = 5$，所以$\triangle AOB$是等腰三角形。对于等腰$\triangle AOB$，以$AB$为底边，$AB$边上的高就是$A$（或$B$）的纵坐标的绝对值，即高$h = 4$，根据三角形面积公式$S=\frac{1}{2}\times底\times高$，这里底$AB = 6$，高$h = 4$，所以$S_{\triangle AOB}=\frac{1}{2}\times6\times4 = 12$。
【答案】：等腰三角形；$12$

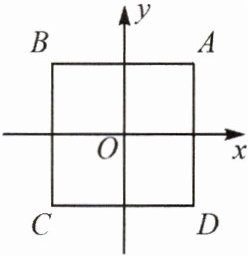
4. 如图，$x$轴、$y$轴为正方形$ABCD$的对称轴，若正方形的边长为$1$，则各顶点的坐标分别是$A$($\frac{1}{2},\frac{1}{2}$)，$B$($-\frac{1}{2},\frac{1}{2}$)，$C$($-\frac{1}{2},-\frac{1}{2}$)，$D$($\frac{1}{2},-\frac{1}{2}$)。

答案： 【解析】：
已知$x$轴、$y$轴为正方形$ABCD$的对称轴，正方形边长为$1$。
因为对称轴将边长平分，所以点$A$在第一象限，横坐标为$\frac{1}{2}$，纵坐标为$\frac{1}{2}$，即$A(\frac{1}{2},\frac{1}{2})$；
点$B$在第二象限，横坐标为$-\frac{1}{2}$，纵坐标为$\frac{1}{2}$，即$B(-\frac{1}{2},\frac{1}{2})$；
点$C$在第三象限，横坐标为$-\frac{1}{2}$，纵坐标为$-\frac{1}{2}$，即$C(-\frac{1}{2},-\frac{1}{2})$；
点$D$在第四象限，横坐标为$\frac{1}{2}$，纵坐标为$-\frac{1}{2}$，即$D(\frac{1}{2},-\frac{1}{2})$。
【答案】：$A(\frac{1}{2},\frac{1}{2})$，$B(-\frac{1}{2},\frac{1}{2})$，$C(-\frac{1}{2},-\frac{1}{2})$，$D(\frac{1}{2},-\frac{1}{2})$。