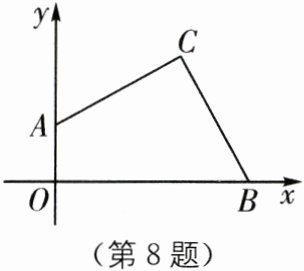
8. (2024·南京玄武区模拟)如图,在平面直角坐标系中,$C(4,4)$,点$B,A分别在x轴正半轴和y$轴正半轴上,$∠ACB= 90^{\circ}$,则$OA+OB$等于( ).
A.8
B.9
C.10
D.11

A.8
B.9
C.10
D.11
答案:
A [解析]过点C作CM⊥y轴于点M,CN⊥x轴于点N,如图,则∠CMA=∠CNB=90°.
∵C(4,4),
∴CN=CM=4.
∵∠MON=∠CNO=∠CMO=90°,
∴∠MCN=360°−90°−90°−90°=90°.
∵∠ACB=90°,
∴∠ACB=∠MCN,
∴∠ACM=∠BCN.在△ACM和△BCN中,∠CMA=∠CNB,CM=CN,∠ACM=∠BCN,
∴△ACM≌△BCN(ASA),
∴AM=BN,
∴OA+OB=OA+ON+BN=OA+ON+AM=ON+OM=4+4=8.故选A.关键提醒 本题考查了全等三角形的判定与性质,四边形的内角和定理,坐标与图形性质等知识,证明三角形全等是解题的关键,
∵C(4,4),
∴CN=CM=4.
∵∠MON=∠CNO=∠CMO=90°,
∴∠MCN=360°−90°−90°−90°=90°.
∵∠ACB=90°,
∴∠ACB=∠MCN,
∴∠ACM=∠BCN.在△ACM和△BCN中,∠CMA=∠CNB,CM=CN,∠ACM=∠BCN,
∴△ACM≌△BCN(ASA),
∴AM=BN,
∴OA+OB=OA+ON+BN=OA+ON+AM=ON+OM=4+4=8.故选A.关键提醒 本题考查了全等三角形的判定与性质,四边形的内角和定理,坐标与图形性质等知识,证明三角形全等是解题的关键,
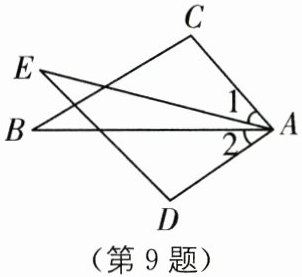
9. (2025·河南洛阳新安期末)如图,已知$∠C= ∠D,AC= AD$,增加下列条件:①$AB= AE$;②$BC= ED$;③$∠1= ∠2$;④$∠B= ∠E$.其中能使$△ABC\cong △AED$的条件有( ).
A.4个
B.3个
C.2个
D.1个

A.4个
B.3个
C.2个
D.1个
答案:
B [解析]①
∵∠C=∠D,AC=AD,AB=AE,
∴△ABC和△AED不一定全等,故①不符合题意;②
∵AC=AD,∠C=∠D,BC=DE,
∴△ABC≌△AED(SAS),故②符合题意;③
∵∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,
∴∠CAB=∠DAE.
∵∠C=∠D,AC=AD,
∴△ABC≌△AED(ASA),故③符合题意;④
∵∠B=∠E,∠C=∠D,AC=AD,
∴△ABC≌△AED(AAS),故④符合题意;故其中能使△ABC≌△AED的条件有3个.故选B.
∵∠C=∠D,AC=AD,AB=AE,
∴△ABC和△AED不一定全等,故①不符合题意;②
∵AC=AD,∠C=∠D,BC=DE,
∴△ABC≌△AED(SAS),故②符合题意;③
∵∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,
∴∠CAB=∠DAE.
∵∠C=∠D,AC=AD,
∴△ABC≌△AED(ASA),故③符合题意;④
∵∠B=∠E,∠C=∠D,AC=AD,
∴△ABC≌△AED(AAS),故④符合题意;故其中能使△ABC≌△AED的条件有3个.故选B.
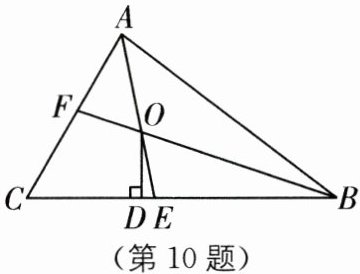
10. (2025·广东广州黄埔区期末)如图,在$△ABC$中,$∠BAC和∠ABC的平分线AE,BF相交于点O$,$AE交BC于E$,$BF交AC于F$,过点$O作OD⊥BC于D$,下列三个结论:①$∠AOB= 90^{\circ}+\frac{1}{2}∠C$;②若$OD= a,AB+BC+CA= b$,则$S_{△ABC}= ab$;③当$∠C= 60^{\circ}$时,$AF+BE= AB$.其中正确的是( ).
A.①②
B.②③
C.①②③
D.①③

A.①②
B.②③
C.①②③
D.①③
答案:
D [解析]
∵△ABC的角平分线AE,BF交于点O,
∴∠OAB=∠OAC=$\frac{1}{2}$∠CAB,∠OBA=∠OBC=$\frac{1}{2}$∠CBA,
∴∠OAB+∠OBA=$\frac{1}{2}$(∠CAB+∠CBA)=$\frac{1}{2}$(180°−∠ACB)=90°−$\frac{1}{2}$∠ACB,
∴∠AOB=180°−(∠OAB+∠OBA)=180°−(90°−$\frac{1}{2}$∠ACB)=90°+$\frac{1}{2}$∠ACB,故①正确;如图
(1),连接OC,作OL⊥AC于点L,OM⊥AB于点M;
∵AE平分∠BAC,BF平分∠ABC,AE交BF于点O,且OD⊥BC于点D,
∴OL=OM=OD=a,
∴S△ABC=S△AOB+S△BOC+S△AOC=$\frac{1}{2}$AB·OM+$\frac{1}{2}$BC·OD+$\frac{1}{2}$CA·OL=$\frac{1}{2}$a(AB+BC+CA).
∵AB+BC+CA=b,
∴S△ABC=$\frac{1}{2}$ab≠ab,故②错误;如图
(2),在AB上截取AH=AF,连接OH,
∵∠C=60°,
∴∠AOB=90°+$\frac{1}{2}$∠C=120°,
∴∠AOF=∠BOE=180°−∠AOB=60°.在△AOH和△AOF中,AH=AF,∠OAH=∠OAF,OA=OA,
∴△AOH≌△AOF(SAS),
∴∠AOH=∠AOF=60°,
∴∠BOH=∠AOB−∠AOH=60°,
∴∠BOH=∠BOE.在△BOH和△BOE中,∠BOH=∠BOE,OB=OB,∠OBH=∠OBE,
∴△BOH≌△BOE(ASA),
∴BH=BE,
∴AF+BE=AH+BH=AB,故③正确.故选D.
∵△ABC的角平分线AE,BF交于点O,
∴∠OAB=∠OAC=$\frac{1}{2}$∠CAB,∠OBA=∠OBC=$\frac{1}{2}$∠CBA,
∴∠OAB+∠OBA=$\frac{1}{2}$(∠CAB+∠CBA)=$\frac{1}{2}$(180°−∠ACB)=90°−$\frac{1}{2}$∠ACB,
∴∠AOB=180°−(∠OAB+∠OBA)=180°−(90°−$\frac{1}{2}$∠ACB)=90°+$\frac{1}{2}$∠ACB,故①正确;如图
(1),连接OC,作OL⊥AC于点L,OM⊥AB于点M;
∵AE平分∠BAC,BF平分∠ABC,AE交BF于点O,且OD⊥BC于点D,
∴OL=OM=OD=a,
∴S△ABC=S△AOB+S△BOC+S△AOC=$\frac{1}{2}$AB·OM+$\frac{1}{2}$BC·OD+$\frac{1}{2}$CA·OL=$\frac{1}{2}$a(AB+BC+CA).
∵AB+BC+CA=b,
∴S△ABC=$\frac{1}{2}$ab≠ab,故②错误;如图
(2),在AB上截取AH=AF,连接OH,
∵∠C=60°,
∴∠AOB=90°+$\frac{1}{2}$∠C=120°,
∴∠AOF=∠BOE=180°−∠AOB=60°.在△AOH和△AOF中,AH=AF,∠OAH=∠OAF,OA=OA,
∴△AOH≌△AOF(SAS),
∴∠AOH=∠AOF=60°,
∴∠BOH=∠AOB−∠AOH=60°,
∴∠BOH=∠BOE.在△BOH和△BOE中,∠BOH=∠BOE,OB=OB,∠OBH=∠OBE,
∴△BOH≌△BOE(ASA),
∴BH=BE,
∴AF+BE=AH+BH=AB,故③正确.故选D.
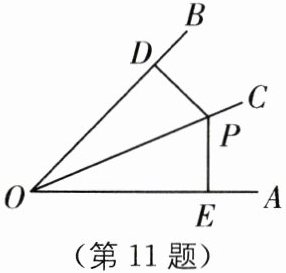
11. (2025·江苏盐城期末)如图,$P是∠AOB的平分线OC$上一点,$PD⊥OB,PE⊥OA$,垂足分别为$D,E$,若$PD= 2$,则$PE$的长是____.

答案:
2 [解析]
∵点P是∠AOB的平分线OC上一点,PD⊥OB,PE⊥OA,PD=2,
∴PE=PD=2.
∵点P是∠AOB的平分线OC上一点,PD⊥OB,PE⊥OA,PD=2,
∴PE=PD=2.
12. (2025·江苏南通如东期末)如图,$D是AB$上一点,$DF交AC于点E,FC// AB$,要使$△ADE\cong △CFE$,只需添加一个条件,则这个条件可以是____.


答案:
AD=CF(答案不唯一) [解析]
∵FC//AB,
∴∠A=∠ECF,∠ADE=∠F.在△ADE和△CFE中,∠A=∠ECF,AD=CF,∠ADE=∠F,
∴△ADE≌△CFE(ASA),
∴要使△ADE≌△CFE,只需添加一个条件,则这个条件可以是AD=CF(答案不唯一).
∵FC//AB,
∴∠A=∠ECF,∠ADE=∠F.在△ADE和△CFE中,∠A=∠ECF,AD=CF,∠ADE=∠F,
∴△ADE≌△CFE(ASA),
∴要使△ADE≌△CFE,只需添加一个条件,则这个条件可以是AD=CF(答案不唯一).
13. 如图,$AE⊥AB且AE= AB,BC⊥CD且BC= CD$,请按照图中所标注的数据,计算图中阴影部分的面积是____.
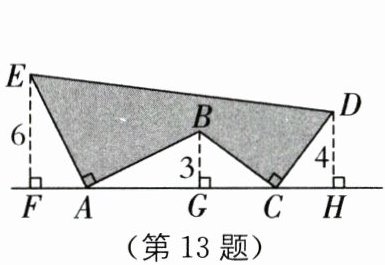

答案:
50 [解析]
∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH,
∴∠EAB=∠EFA=∠BGA=90°,
∴∠EAF+∠BAG=90°,∠ABG+∠BAG=90°,
∴∠EAF=∠ABG.在△EFA与△AGB中,∠EFA=∠AGB,∠EAF=∠ABG,EA=AB,
∴△EFA≌△AGB(AAS),
∴AF=BG=3,EF=AG=6.同理证得△BGC≌△CHD(AAS),得GC=HD=4,BG=CH=3,故FH=FA+AG+GC+CH=3+6+4+3=16,故S阴影=S梯形−2S△EFA−2S△BGC=$\frac{(EF+DH)·FH}{2}$−2×$\frac{1}{2}$EF·AF−2×$\frac{1}{2}$BG·GC=$\frac{1}{2}$×(6+4)×16−6×3−3×4=50.解后反思 本题考查的是全等三角形的判定与性质,关键是把不规则图形的面积转化成规则图形的面积,
∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH,
∴∠EAB=∠EFA=∠BGA=90°,
∴∠EAF+∠BAG=90°,∠ABG+∠BAG=90°,
∴∠EAF=∠ABG.在△EFA与△AGB中,∠EFA=∠AGB,∠EAF=∠ABG,EA=AB,
∴△EFA≌△AGB(AAS),
∴AF=BG=3,EF=AG=6.同理证得△BGC≌△CHD(AAS),得GC=HD=4,BG=CH=3,故FH=FA+AG+GC+CH=3+6+4+3=16,故S阴影=S梯形−2S△EFA−2S△BGC=$\frac{(EF+DH)·FH}{2}$−2×$\frac{1}{2}$EF·AF−2×$\frac{1}{2}$BG·GC=$\frac{1}{2}$×(6+4)×16−6×3−3×4=50.解后反思 本题考查的是全等三角形的判定与性质,关键是把不规则图形的面积转化成规则图形的面积,
14. (2024·广东广州荔湾区期中)如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,若测量得$A'B'= 10cm$,则工件内槽宽$AB$为____$cm$.
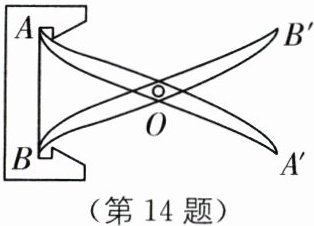

答案:
10
查看更多完整答案,请扫码查看


