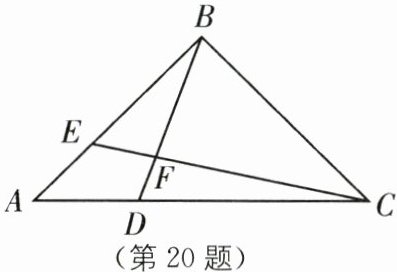
20. (2025·贵州毕节威宁期末)如图,在$\triangle ABC$中,$∠ABD= 24^{\circ },∠A= 45^{\circ },∠ACE= 12^{\circ }$.
(1)求$∠BFC$的度数;
(2)若$∠ABC= 90^{\circ }$,求证:$∠BCF= \frac {1}{2}∠CBF$.
(1)求$∠BFC$的度数;
(2)若$∠ABC= 90^{\circ }$,求证:$∠BCF= \frac {1}{2}∠CBF$.

答案:
(1)
∵∠BFC=∠BEF+∠EBF,∠BEF=∠A+∠ACE,
∴∠BFC=∠A+∠ACE+∠ABD=45°+24°+12°=81°.
(2)
∵∠ABC=90°,∠ABD=24°,
∴∠CBF=∠ABC−∠ABD=66°,
∵∠BFC=81°,
∴∠BCF=180°−81°−66°=33°,
∴∠BCF=$\frac{1}{2}$∠CBF.
(1)
∵∠BFC=∠BEF+∠EBF,∠BEF=∠A+∠ACE,
∴∠BFC=∠A+∠ACE+∠ABD=45°+24°+12°=81°.
(2)
∵∠ABC=90°,∠ABD=24°,
∴∠CBF=∠ABC−∠ABD=66°,
∵∠BFC=81°,
∴∠BCF=180°−81°−66°=33°,
∴∠BCF=$\frac{1}{2}$∠CBF.
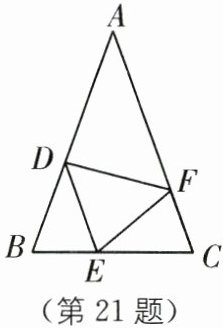
21. (2025·浙江台州期中)如图,在$\triangle ABC$中,$AB= AC$,点$D,E,F分别在AB,BC,AC$边上,且$BE= CF,BD= CE$.
(1)求证:$\triangle DEF$是等腰三角形;
(2)当$∠A= 40^{\circ }$时,求$∠DEF$的度数.
(1)求证:$\triangle DEF$是等腰三角形;
(2)当$∠A= 40^{\circ }$时,求$∠DEF$的度数.

答案:
(1)
∵AB=AC,
∴∠ABC=∠ACB.在△DBE和△ECF中,{BE=CF,∠ABC=∠ACB,BD=CE,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴△DEF是等腰三角形.
(2)
∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4.
∵∠A+∠B+∠C=180°,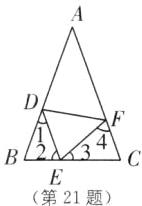
∴∠B=$\frac{1}{2}$×(180°−40°)=70°,
∴∠1+∠2=110°,
∴∠3+∠2=110°,
∴∠DEF=70°.
(1)
∵AB=AC,
∴∠ABC=∠ACB.在△DBE和△ECF中,{BE=CF,∠ABC=∠ACB,BD=CE,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴△DEF是等腰三角形.
(2)
∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4.
∵∠A+∠B+∠C=180°,

∴∠B=$\frac{1}{2}$×(180°−40°)=70°,
∴∠1+∠2=110°,
∴∠3+∠2=110°,
∴∠DEF=70°.
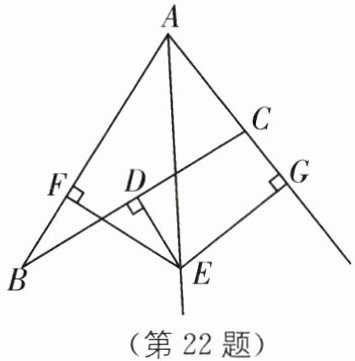
22. 如图,已知$D是BC$的中点,过点$D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G$.
(1)求证:$BF= CG$;
(2)若$AB= 10,AC= 6$,求线段$CG$的长.
(1)求证:$BF= CG$;
(2)若$AB= 10,AC= 6$,求线段$CG$的长.

答案:
(1)如图,连接EC,EB.
∵AE是∠CAB的平分线,EF⊥AB于点F,EG⊥AC于点G,
∴EG=EF.又ED垂直平分BC,
∴EC=EB.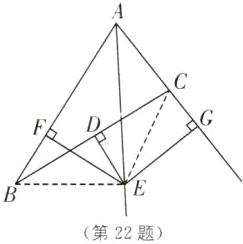
∴Rt△CGE≌Rt△BFE(HL).
∴BF=CG.
(2)在Rt△AEF和Rt△AEG中,{AE=AE,EF=EG,
∴Rt△AEF≌Rt△AEG(HL).
∴AF=AG.
∵BF=CG,
∴AB+AC=AF+BF+AG−CG=2AG.
∵AB=10,AC=6,
∴AG=8.
∴CG=AG−AC=2.
(1)如图,连接EC,EB.
∵AE是∠CAB的平分线,EF⊥AB于点F,EG⊥AC于点G,
∴EG=EF.又ED垂直平分BC,
∴EC=EB.

∴Rt△CGE≌Rt△BFE(HL).
∴BF=CG.
(2)在Rt△AEF和Rt△AEG中,{AE=AE,EF=EG,
∴Rt△AEF≌Rt△AEG(HL).
∴AF=AG.
∵BF=CG,
∴AB+AC=AF+BF+AG−CG=2AG.
∵AB=10,AC=6,
∴AG=8.
∴CG=AG−AC=2.
查看更多完整答案,请扫码查看


