《2025年实验班提优训练八年级数学上册人教版》

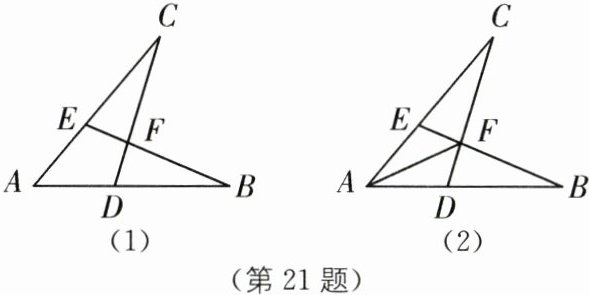
21. (2025·河北廊坊安次区期末)如图(1),已知$AB= AC,AD= AE$.
(1)求证:$△ACD\cong △ABE$.
(2)图(1)中还有没有其他全等的三角形? 若有请写出并说明理由.
(3)如图(2),连接$AF,AF是不是∠CAB$的平分线? 请说明理由.

答案：
(1)在△ACD和△ABE中,AC=AB,∠A=∠A,AD=AE,
∴△ACD≌△ABE(SAS).
(2)还有△BDF≌△CEF,理由如下:
∵AB=AC,AD=AE.
∴AB−AD=AC−AE,即BD=CE.由
(1)可知△ACD≌△ABE,
∴∠B=∠C.在△BDF和△CEF中,∠BFD=∠CFE,∠B=∠C,BD=CE,
∴△BDF≌△CEF(AAS).
(3)AF是∠CAB的平分线,理由如下:由
(2)可知△BDF≌△CEF,
∴DF=EF.在△ADF和△AEF中,AD=AE,DF=EF,AF=AF,
∴△ADF≌△AEF(SSS),
∴∠DAF=∠EAF,
∴AF是∠CAB的平分线.

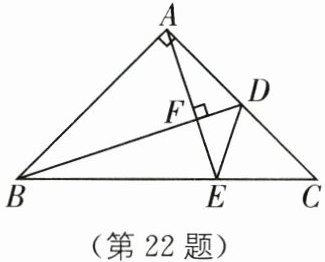
22. 如图,在$△ABC$中,$∠BAC= 90^{\circ}$,且$AB= AC,∠ABC= ∠ACB= 45^{\circ}$,点$D是AC$的中点,$AE⊥BD于点F$,交$BC于点E$,连接$DE$.求证:$∠ADB= ∠EDC$.

答案： 如图，过点C作CM⊥AC,交AE的延长线于点M,则∠ACM=90°=∠BAC,
∴CM//AB.
∴∠MCE=∠ABC=∠ACB.
∵AE⊥BD,∠BAC=90°,
∴∠CAM+∠BAF=90°,∠ABD+∠BAF=90°,
∴∠ABD=∠CAM.在△ABD和△CAM中,∠DAB=∠MCA,AB=CA,∠ABD=∠CAM,
∴△ABD≌△CAM(ASA).
∴∠ADB=∠M,AD=CM.
∵D为AC的中点，
∴AD=DC=CM.在△CDE和△CME中,CD=CM,∠DCE=∠MCE,CE=CE,
∴△CDE≌△CME(SAS).
∴∠M=∠EDC,
∴∠ADB=∠EDC.