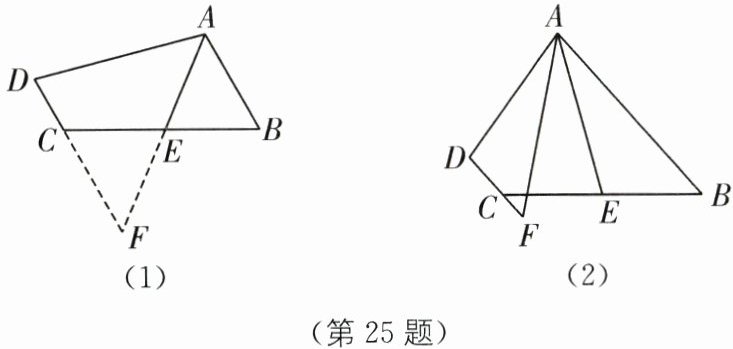
25. (1)如图(1),在四边形$ABCD$中,$AB// CD$,点$E是BC$的中点,若$AE是∠BAD$的平分线,试判断$AB,AD,DC$之间的等量关系.
解决此问题可以用如下方法:延长$AE交DC的延长线于点F$,易证$\triangle AEB\cong \triangle FEC$,得到$AB= FC$,从而把$AB,AD,DC$转化在一个三角形中即可判断.$AB,AD,DC$之间的等量关系为______.
(2)问题探究:如图(2),在四边形$ABCD$中,$AB// CD,AF与DC的延长线交于点F$,点$E是BC$的中点,若$AE是∠BAF$的平分线,试探究$AB,AF,CF$之间的等量关系,并证明你的结论.
解决此问题可以用如下方法:延长$AE交DC的延长线于点F$,易证$\triangle AEB\cong \triangle FEC$,得到$AB= FC$,从而把$AB,AD,DC$转化在一个三角形中即可判断.$AB,AD,DC$之间的等量关系为______.
(2)问题探究:如图(2),在四边形$ABCD$中,$AB// CD,AF与DC的延长线交于点F$,点$E是BC$的中点,若$AE是∠BAF$的平分线,试探究$AB,AF,CF$之间的等量关系,并证明你的结论.

答案:
(1)AD=AB+DC [解析]
∵AB//CD,
∴∠F=∠BAE.
∵点E是BC的中点,
∴CE=BE.又∠F=∠BAE,∠CEF=∠AEB,
∴△CEF≌△BEA(AAS).
∴AB=CF.
∵AE是∠BAD的平分线,
∴∠DAF=∠BAE.
∴∠DAF=∠F.
∴AD=DF.
∴AD=CF+CD=AB+CD.
(2)AB=AF+CF,证明如下:如图,延长AE交DF的延长线于点G.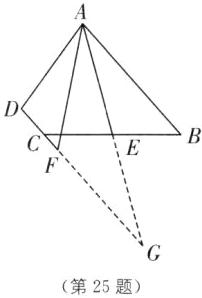
∵E是BC的中点,
∴CE=BE.
∵AB//DC,
∴∠BAE=∠G.又∠AEB=∠GEC,BE=CE,
∴△AEB≌△GEC(AAS).
∴AB=GC.
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG.又∠BAG=∠G,
∴∠FAG=∠G.
∴FA=FG.
∵CG=FG+CF,
∴AB=AF+CF.
(1)AD=AB+DC [解析]
∵AB//CD,
∴∠F=∠BAE.
∵点E是BC的中点,
∴CE=BE.又∠F=∠BAE,∠CEF=∠AEB,
∴△CEF≌△BEA(AAS).
∴AB=CF.
∵AE是∠BAD的平分线,
∴∠DAF=∠BAE.
∴∠DAF=∠F.
∴AD=DF.
∴AD=CF+CD=AB+CD.
(2)AB=AF+CF,证明如下:如图,延长AE交DF的延长线于点G.

∵E是BC的中点,
∴CE=BE.
∵AB//DC,
∴∠BAE=∠G.又∠AEB=∠GEC,BE=CE,
∴△AEB≌△GEC(AAS).
∴AB=GC.
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG.又∠BAG=∠G,
∴∠FAG=∠G.
∴FA=FG.
∵CG=FG+CF,
∴AB=AF+CF.
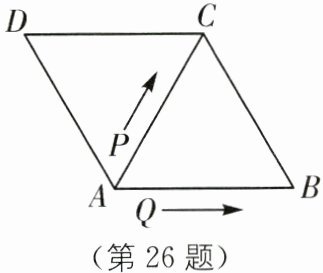
26. (2025·浙江杭州期中)如图所示,$\triangle ABC和\triangle ACD$都是边长为4厘米等边三角形,两个动点$P,Q同时从A$点出发,点$P$以1厘米/秒的速度沿$A→C→B$的方向运动,点$Q$以2厘米/秒的速度沿$A→B→C→D$的方向运动,当点$Q运动到D$点时,$P,Q$两点同时停止运动.设$P,Q运动的时间为t$秒.
(1)点$P,Q$从出发到相遇所用时间是______秒.
(2)当$t$取何值时,$\triangle APQ$也是等边三角形? 请说明理由.
(3)当$0<t<2$时,判断$PQ与AC$的位置关系.
(1)点$P,Q$从出发到相遇所用时间是______秒.
(2)当$t$取何值时,$\triangle APQ$也是等边三角形? 请说明理由.
(3)当$0<t<2$时,判断$PQ与AC$的位置关系.

答案:
(1)4 [解析]设点P,Q从出发到相遇所用时间是t,根据题意,得t+2t=AC+AB+BC=12,解得t=4.
(2)如图
(1),若△APQ是等边三角形,此时点P在BC上,点Q在CD上,且易证△ADQ≌△ACP,则CP=DQ,即t−4=4−(2t−8),解得t=$\frac{16}{3}$.
(3)PQ与AC互相垂直,理由如下:如图
(2)所示,根据题意,得AQ=2AP,取AQ的中点N,则AN=NQ=AP.
∵∠PAQ=60°,
∴△APN是等边三角形,
∴PN=AN=NQ,∠ANP=60°,
∴∠NPQ=∠NQP =30°,
∴∠APQ=90°,即当0<t<2时,PQ与AC互相垂直.
(1)4 [解析]设点P,Q从出发到相遇所用时间是t,根据题意,得t+2t=AC+AB+BC=12,解得t=4.
(2)如图
(1),若△APQ是等边三角形,此时点P在BC上,点Q在CD上,且易证△ADQ≌△ACP,则CP=DQ,即t−4=4−(2t−8),解得t=$\frac{16}{3}$.
(3)PQ与AC互相垂直,理由如下:如图
(2)所示,根据题意,得AQ=2AP,取AQ的中点N,则AN=NQ=AP.
∵∠PAQ=60°,
∴△APN是等边三角形,
∴PN=AN=NQ,∠ANP=60°,
∴∠NPQ=∠NQP =30°,
∴∠APQ=90°,即当0<t<2时,PQ与AC互相垂直.

查看更多完整答案,请扫码查看


